Mathematics
If radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other is
3 cm
6 cm
9 cm
1 cm
Circles
4 Likes
Answer
From figure,
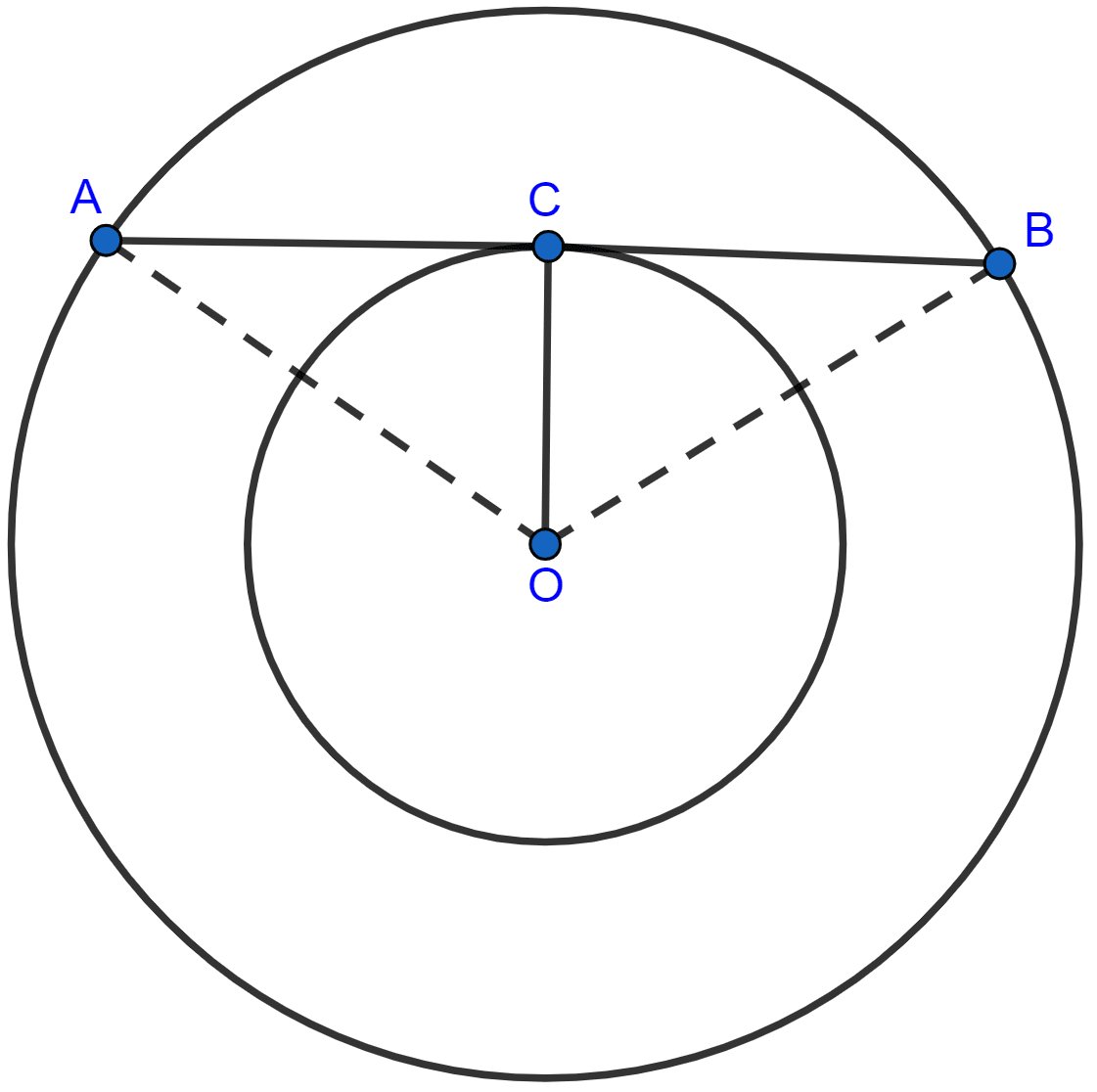
AB is chord to the bigger circle which is tangent to the smaller circle at C.
OC ⊥ AC (∵ radius of a circle and tangent through that point are perpendicular to each other.)
∴ ∠ACO = 90°.
In △ACO,
Length of chord AB = 2 × AC = 2 × 3 = 6 cm.
Hence, Option 2 is the correct option.
Answered By
2 Likes
Related Questions
In the adjoining figure, PA and PB are tangents from point P to a circle with centre O. If the radius of the circle is 5 cm and PA ⊥ PB, then the length OP is equal to
5 cm
10 cm
7.5 cm
5√2 cm

At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is
4 cm
5 cm
6 cm
8 cm
In the adjoining figure, O is the centre of a circle and PQ is a chord. If the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is
100°
80°
90°
75°

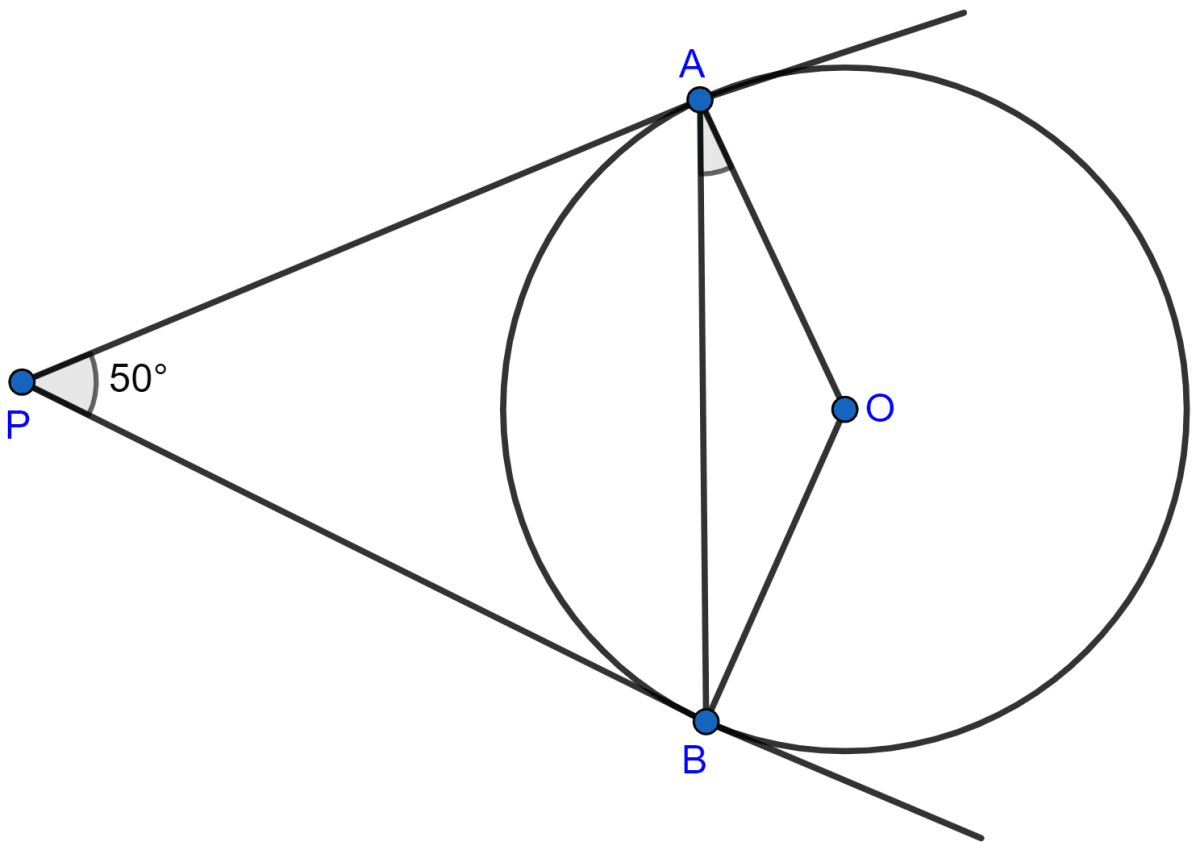
In the adjoining figure, PA and PB are tangents to a circle with centre O. If ∠APB = 50°, then ∠OAB is equal to
25°
30°
40°
50°