Mathematics
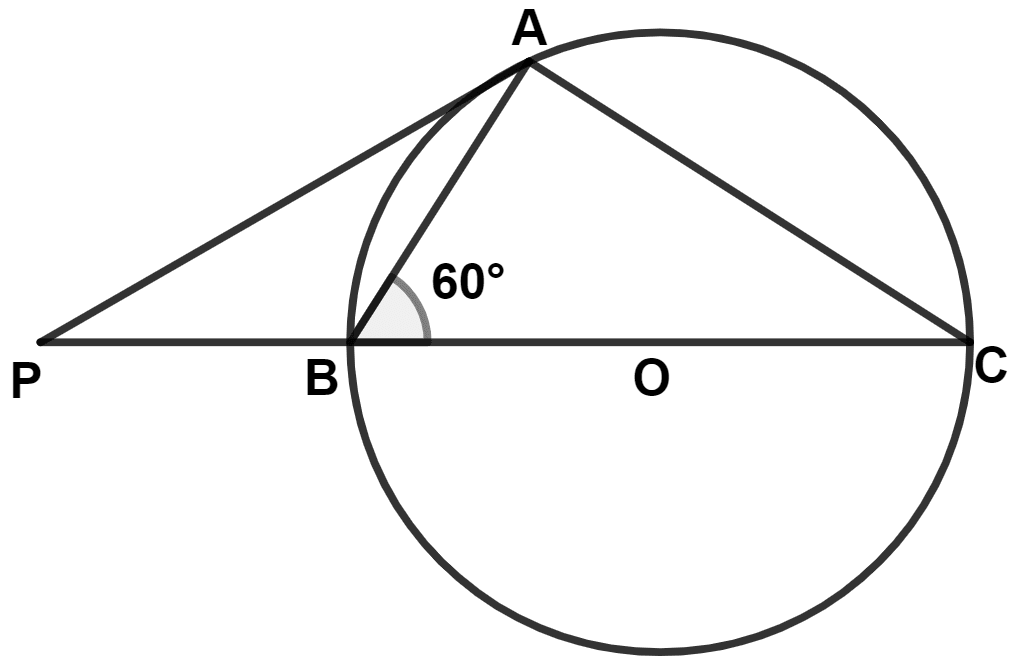
If ∠PAC : ∠PCA = 4 : 5, ∠P is :
40°
60°
105°
45°

Circles
8 Likes
Answer
We know that,
Sum of co-interior angles in a trapezium is 180°.
In trapezium ABDC,
⇒ ∠B + ∠BAC = 180°
⇒ 60° + ∠BAC = 180°
⇒ ∠BAC = 180° - 60° = 120°.
From figure,
⇒ ∠PAC + ∠BAC = 180°
⇒ ∠PAC + 120° = 180°
⇒ ∠PAC = 180° - 120° = 60°.
Given,
⇒ ∠PAC : ∠PCA = 4 : 5
In △PCA,
By angle sum property of triangle,
⇒ ∠APC + ∠PAC + ∠PCA = 180°
⇒ ∠APC + 60° + 75° = 180°
⇒ ∠APC + 135° = 180°
⇒ ∠APC = 180° - 135° = 45°.
Hence, Option 4 is the correct option.
Answered By
4 Likes
Related Questions
In the given circle, PA is tangent and PBC is secant, PA = 8 cm and PB = 4 cm. The length of BC is :
8 cm
12 cm
16 cm
2 cm

AC is a tangent to the given circle which touches the circle at point B. If ∠EBC = 45°; angle EDB is equal to :
45°
90°
125°
135°

In the given figure, O is the center of the circle, PA is tangent and PBC is secant. If ∠ABC = 60°; ∠P is :
30°
60°
120°
90°
Chords AB and CD of a circle intersect each other at point O such that OA : OC = 4 : 7. Then OB : OD is equal to :
4 : 7
5 : 4
7 : 4
4 : 5
