Mathematics
If each diagonal of a quadrilateral divides it into two triangles of equal areas, then prove that the quadrilateral is a parallelogram.
Theorems on Area
3 Likes
Answer
Let ABCD be a quadrilateral such that each diagonal divides it into triangles of equal areas, then
area of △ABC = Area of ABCD, …….(1)
area of △ABD = Area of ABCD, ……(2)
area of △BCD = Area of ABCD, …….(3)
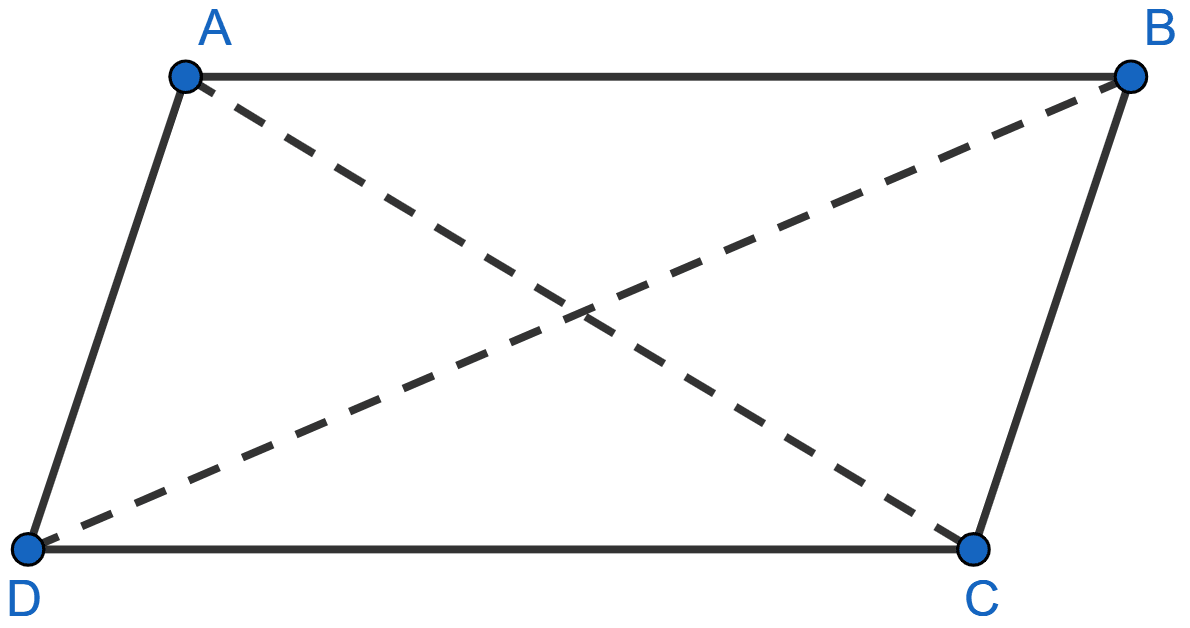
We know that,
Triangles on the same base and having equal areas lie between the same parallel lines.
From (1) and (2) we get,
Area of △ABC = Area of △ABD.
Since, △ABC and △ABD lie on same base AB and have equal area.
So, AB || CD.
From (1) and (3) we get,
∴ Area of △ABC = Area of △BCD.
Since, △ABC and △BCD lie on same base BC and have equal area.
So, BC || AD.
Since, AB || CD and BC || AD.
Hence, proved ABCD is a parallelogram.
Answered By
2 Likes
Related Questions
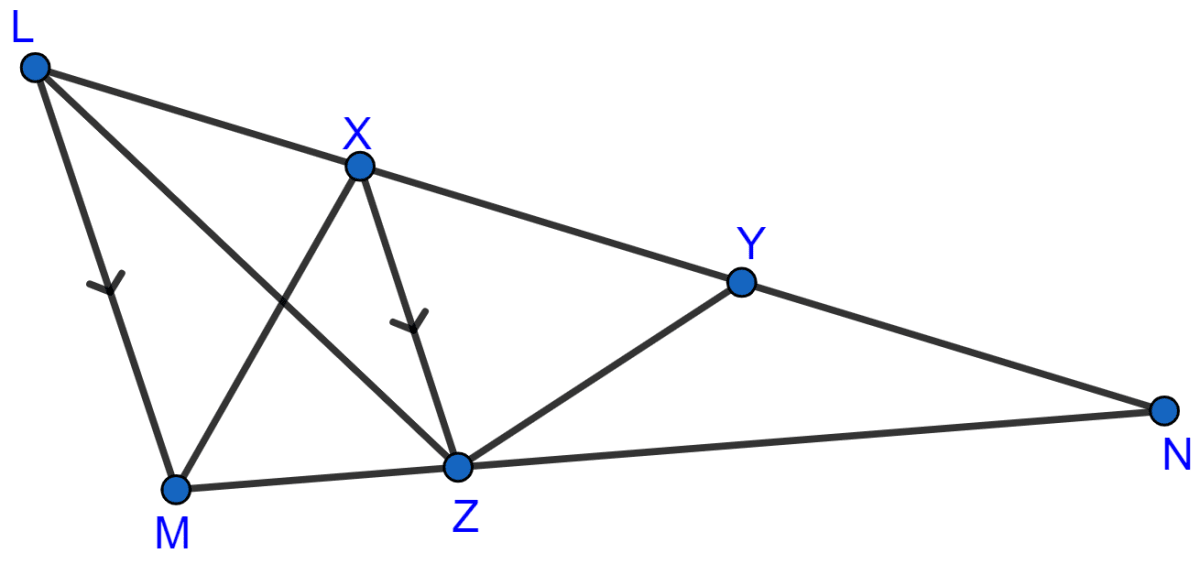
In the adjoining figure, X and Y are points on the side LN of triangle LMN. Through X, a line is drawn parallel to LM to meet MN at Z. Prove that area of ∆LZY = area of quad. MZYX.
Perpendiculars are drawn from a point within an equilateral triangle to the three sides. Prove that the sum of the three perpendiculars is equal to the altitude of the triangle.
In the adjoining figure, ABCD is a square. E and F are mid-points of sides BC and CD respectively. If R is mid-point of EF, prove that:
area of ∆AER = area of ∆AFR

In the adjoining figure, ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F. If area of ∆DFB = 3 cm2, find the area of parallelogram ABCD.
