Mathematics
If AD, BE and CF are medians of △ABC, prove that
3(AB2 + BC2 + CA2) = 4(AD2 + BE2 + CF2).
Related Questions
In the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O, at right angles. Prove that AB2 + CD2 = AD2 + BC2.

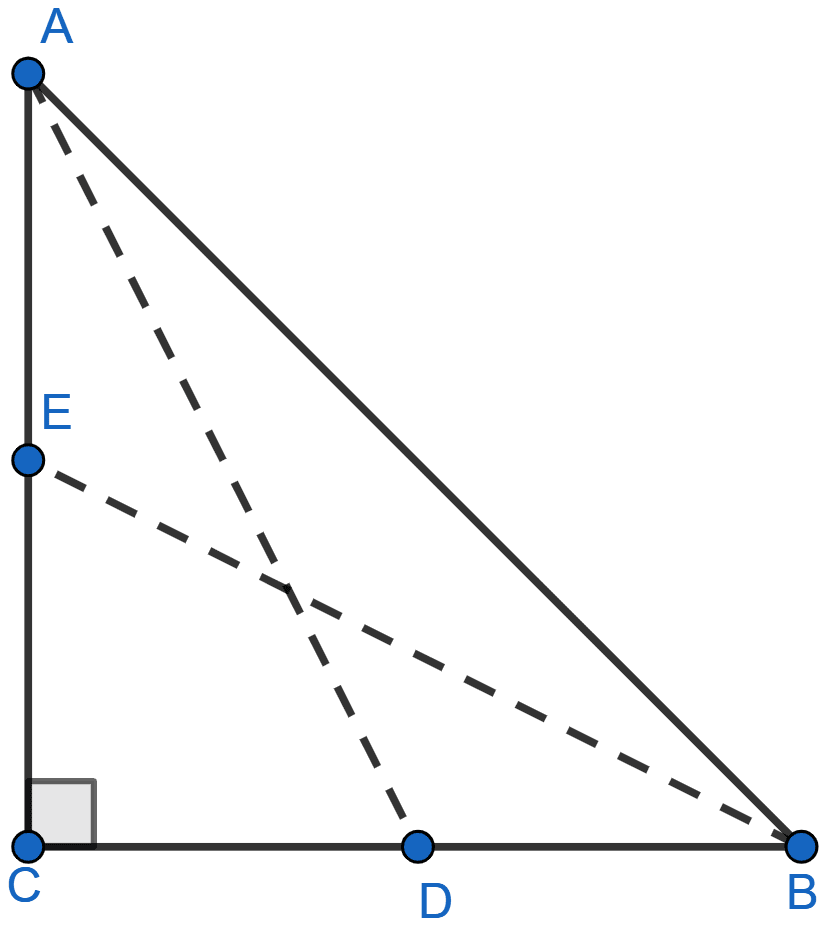
In the adjoining figure, D and E are mid-points of the sides BC and CA respectively of a △ABC, right angled at C. Prove that :
(i) 4AD2 = 4AC2 + BC2
(ii) 4BE2 = 4BC2 + AC2
(iii) 4(AD2 + BE2) = 5AB2
In a quadrilateral ABCD, ∠B = 90° = ∠D. Prove that
2AC2 - BC2 = AB2 + AD2 + DC2.
AD is perpendicular to the side BC of an equilateral △ABC. Prove that 4AD2 = 3AB2.