Mathematics
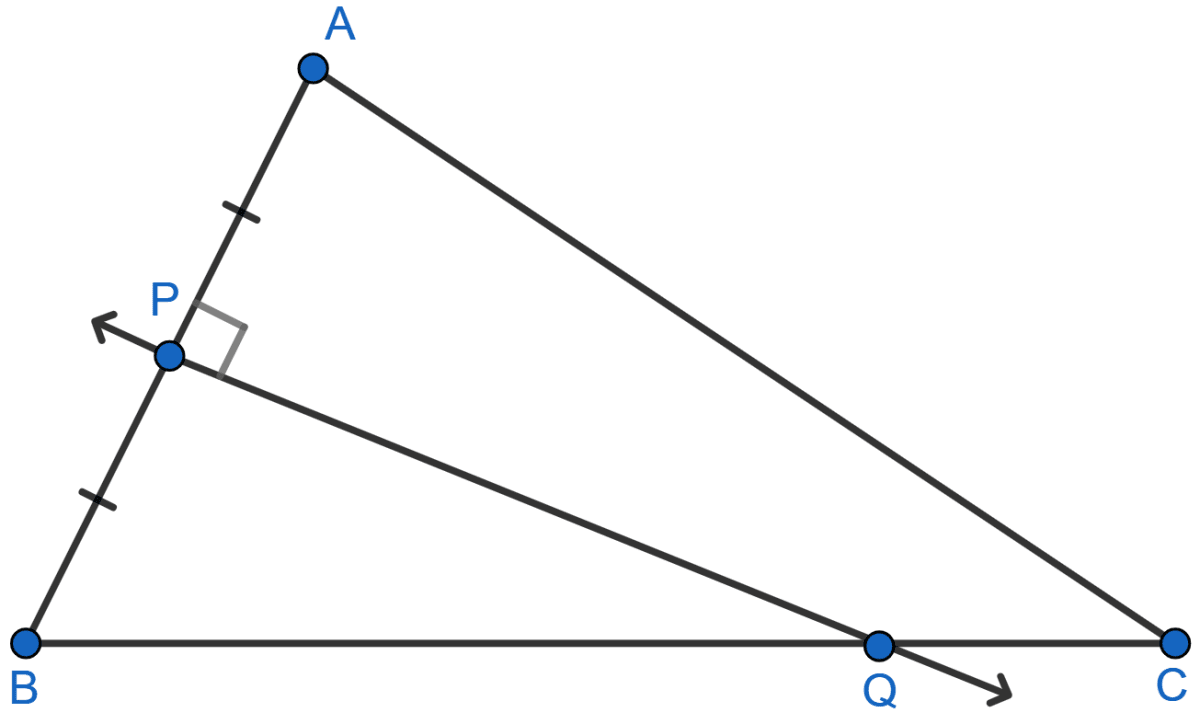
Given: PQ is a perpendicular bisector of side AB of the triangle ABC.
Prove: Q is equidistant from A and B.
Locus
15 Likes
Answer
Join A and Q as shown in the figure below:
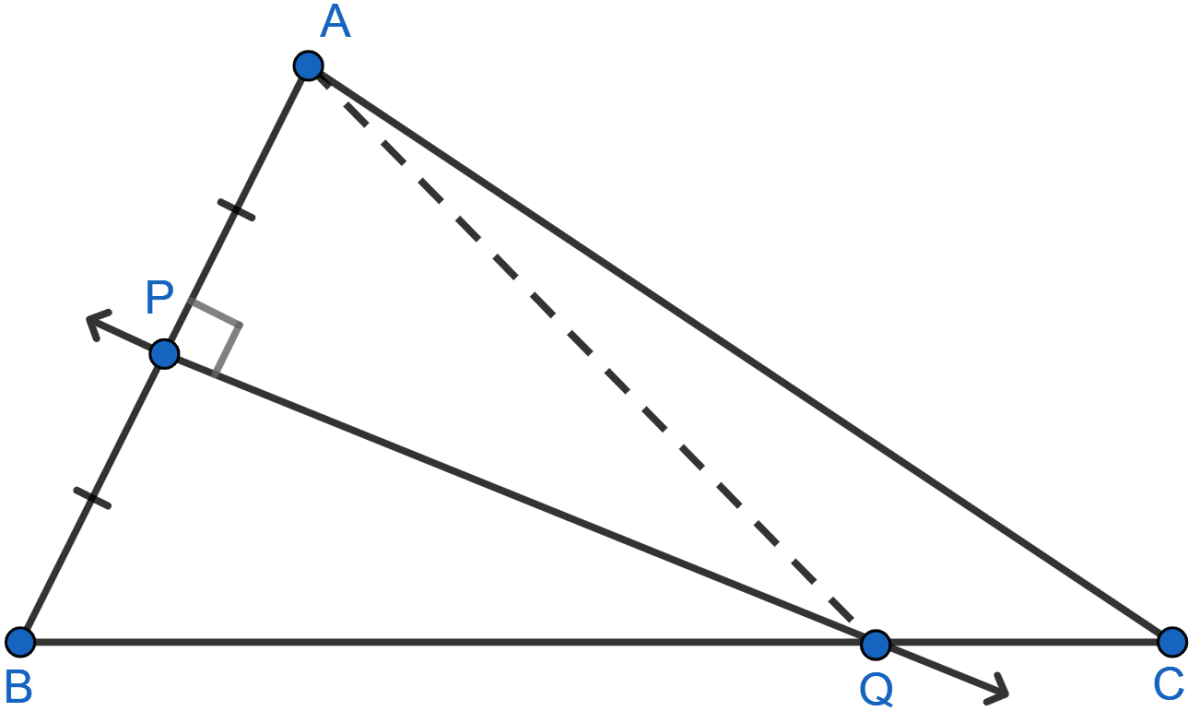
In ∆AQP and ∆BQP,
⇒ AP = BP [Given]
⇒ ∠QPA = ∠QPB [Each 90°]
⇒ PQ = PQ [Common]
∴ ∆AQP ≅ ∆BQP by SAS axiom.
∴ AQ = BQ [By C.P.C.T.]
Hence, proved that Q is equidistant from A and B.
Answered By
9 Likes
Related Questions
Bisector of angle B of triangle ABC intersects side AC at point P, then point P is :
equidistant from vertices A and C
PA = PB
PB = PC
equidistant from sides AB and BC
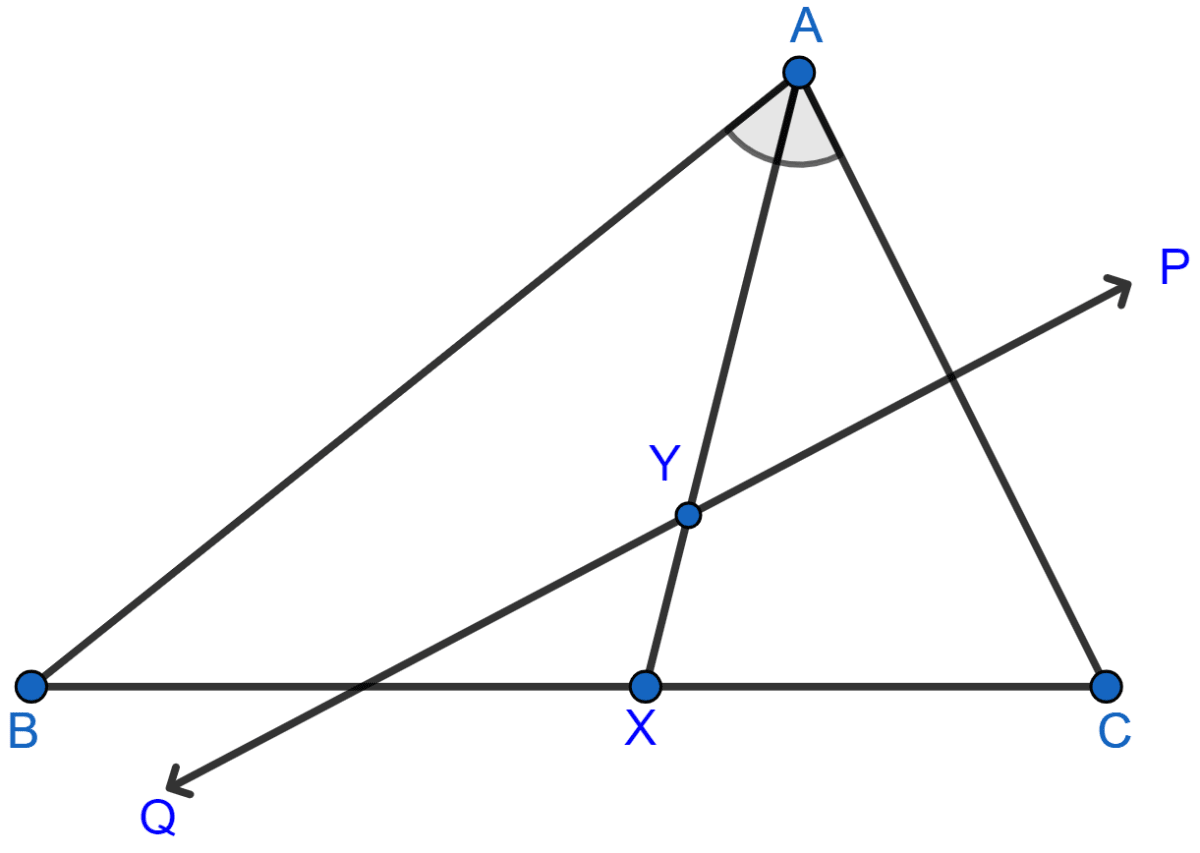
Given: AX bisects angle BAC and PQ is perpendicular bisector of AC which meets AX at point Y.
Prove :
(i) X is equidistant from AB and AC.
(ii) Y is equidistant from A and C.
Given: CP is the bisector of angle C of ∆ABC.
Prove: P is equidistant from AC and BC.

Using the information in the given diagram, state if :

AD = DC
BD = DC
CD bisects angle ACB
angle CAD is greater than angle DAB