Given points A(1, 5), B(-3, 7) and C(15, 9).

(i) Find the equation of a line passing through the mid-point of AC and the point B.

(ii) Find the equation of the line through C and parallel to AB.

(iii) The lines obtained in part (i) and (ii) above, intersect each other at a point P. Find the coordinates of the point P.

(iv) Assign, giving reason, a special name of the figure PABC.

(i) By formula,

Mid-point (M) = $\Big(\dfrac{m$1x2 + m2x1}{m1 + m2}, \dfrac{m1y2 + m2y1}{m1 + m2}\Big)

Let D be the mid-point of AC.

D = $\Big(\dfrac{1 + 15}{2}, \dfrac{5 + 9}{2}\Big) = \Big(\dfrac{16}{2}, \dfrac{14}{2}\Big)$ = (8, 7).

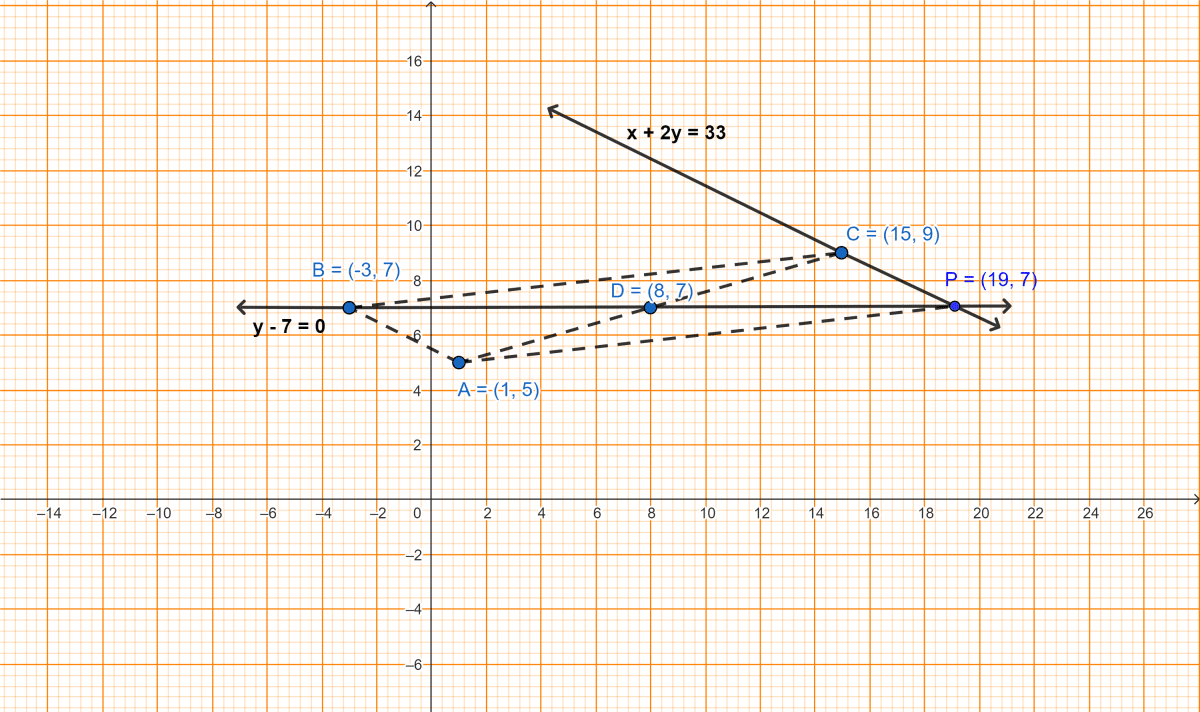
By two-point formula,

Equation of straight line :

⇒ y - y₁ = $\dfrac{y$2 - y1}{x2 - x1}(x - x₁)

Equation of BD :

$\Rightarrow y - 7 = \dfrac{7 - 7}{8 - (-3)}[x - (-3)] \\[1em] \Rightarrow y - 7 = 0 \times (x + 3) \\[1em] \Rightarrow y - 7 = 0.$

Hence, equation of a line passing through the mid-point of AC and the point B is y - 7 = 0.

(ii) By formula,

Slope = $\dfrac{y$2 - y1}{x2 - x1}

Slope of AB = $\dfrac{7 - 5}{-3 - 1} = -\dfrac{2}{4} = -\dfrac{1}{2}$.

As, slope of parallel lines are equal.

∴ Slope of line parallel to AB = -$\dfrac{1}{2}$.

By point-slope form, equation :

$y - y$1 = m(x - x1)

Slope of line through C and parallel to AB.

$\Rightarrow y - 9 = -\dfrac{1}{2}(x - 15) \\[1em] \Rightarrow 2(y - 9) = -1(x - 15) \\[1em] \Rightarrow 2y - 18 = -x + 15 \\[1em] \Rightarrow x + 2y = 15 + 18 \\[1em] \Rightarrow x + 2y = 33.$

Hence, equation of the line through C and parallel to AB is x + 2y = 33.

(iii) Equations are :

⇒ y - 7 = 0 ……….(1)

⇒ x + 2y = 33 ………(2)

From equation (1),

⇒ y = 7 ……..(3)

Substituting above value of y in equation (2), we get :

⇒ x + 2(7) = 33

⇒ x + 14 = 33

⇒ x = 33 - 14 = 19.

∴ P = (x, y) = (19, 7).

Hence, P = (19, 7).

(iv) Steps :

1. Mark points A, B, C and P.

2. Join AB, BC, CP and PA.

3. From graph, PABC is a trapezium.

Hence, PABC is a trapezium.