Mathematics
Given: CP is the bisector of angle C of ∆ABC.
Prove: P is equidistant from AC and BC.

Locus
12 Likes
Answer
From P, draw PL ⊥ AC and PM ⊥ CB

In ∆LPC and ∆MPC,
⇒ ∠PLC = ∠PMC [Each 90°]
⇒ ∠PCL = ∠MCP [Since, CP is bisector of angle C]
⇒ PC = PC [Common]
∴ ∆LPC ≅ ∆MPC by AAS axiom.
∴ PL = PM [By C.P.C.T.]
Hence, proved that P is equidistant from AC and BC.
Answered By
8 Likes
Related Questions
Bisector of angle B of triangle ABC intersects side AC at point P, then point P is :
equidistant from vertices A and C
PA = PB
PB = PC
equidistant from sides AB and BC
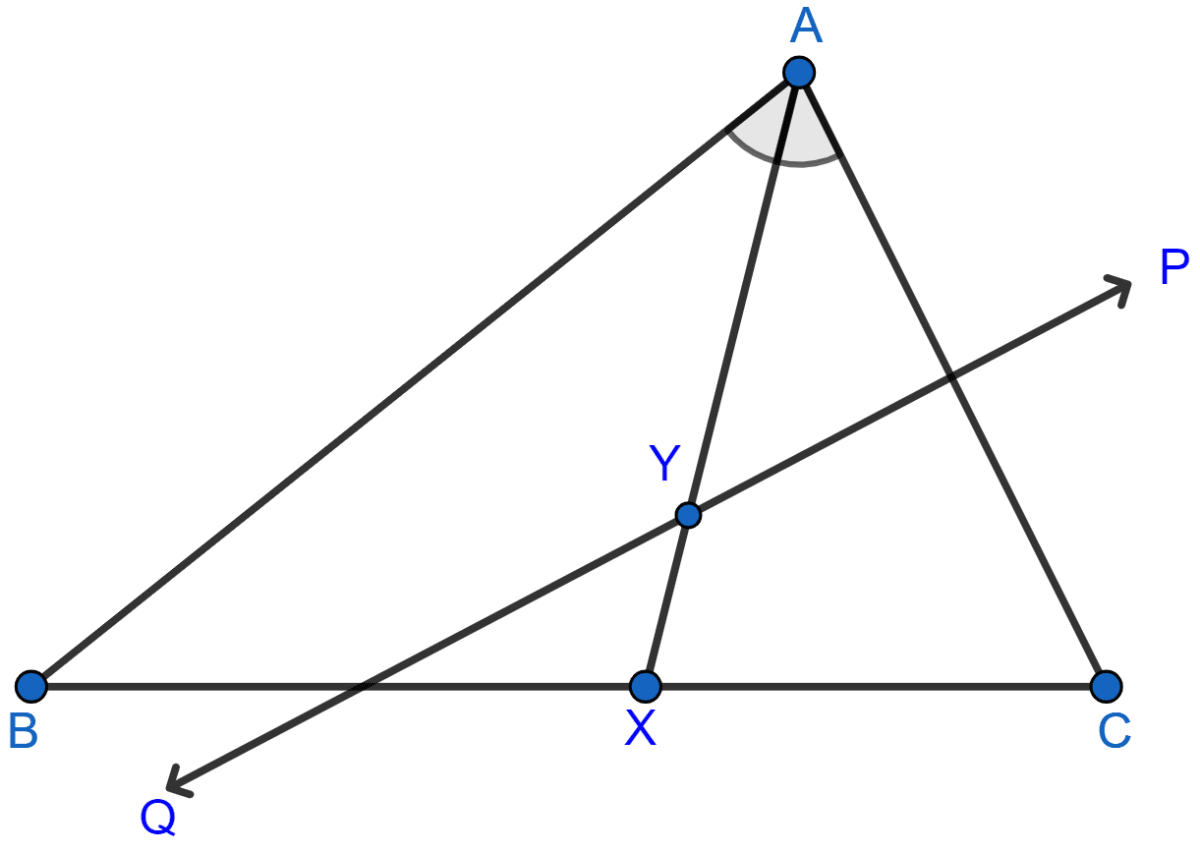
Given: AX bisects angle BAC and PQ is perpendicular bisector of AC which meets AX at point Y.
Prove :
(i) X is equidistant from AB and AC.
(ii) Y is equidistant from A and C.
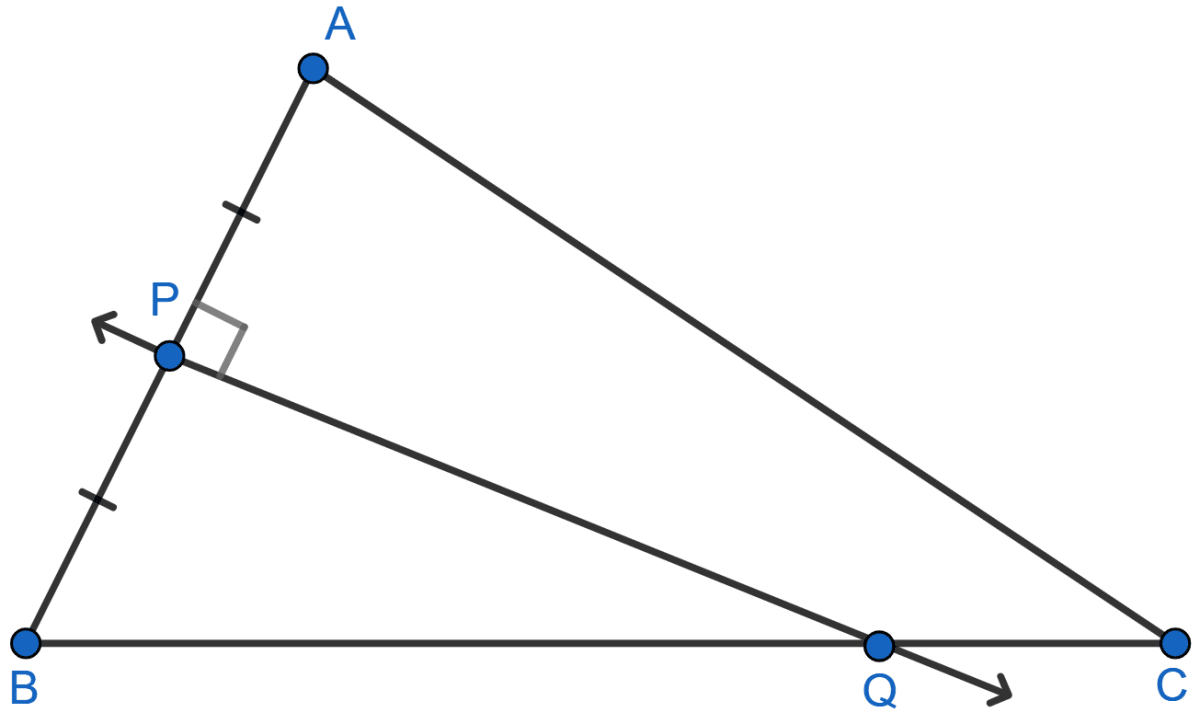
Given: PQ is a perpendicular bisector of side AB of the triangle ABC.
Prove: Q is equidistant from A and B.
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.