Mathematics
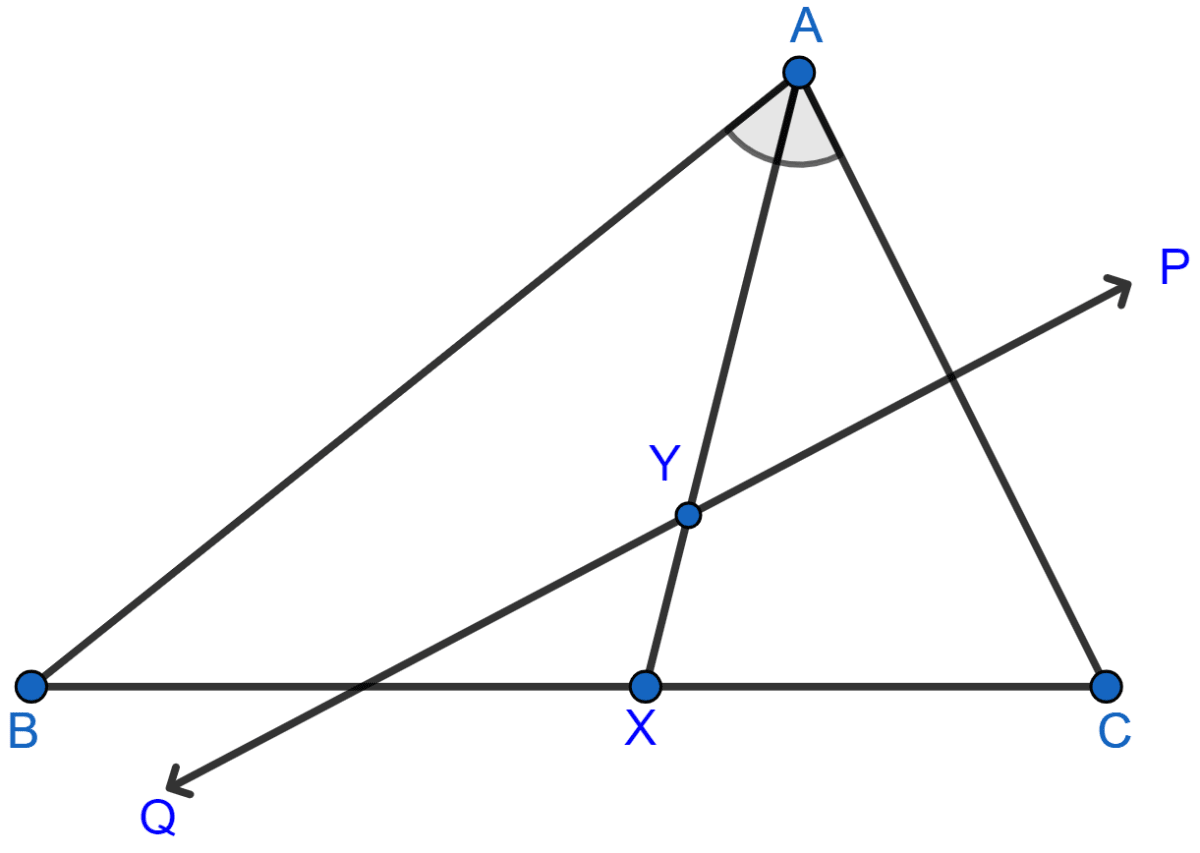
Given: AX bisects angle BAC and PQ is perpendicular bisector of AC which meets AX at point Y.
Prove :
(i) X is equidistant from AB and AC.
(ii) Y is equidistant from A and C.
Answer
From X, draw XL ⊥ AC and XM ⊥ AB and join YC.
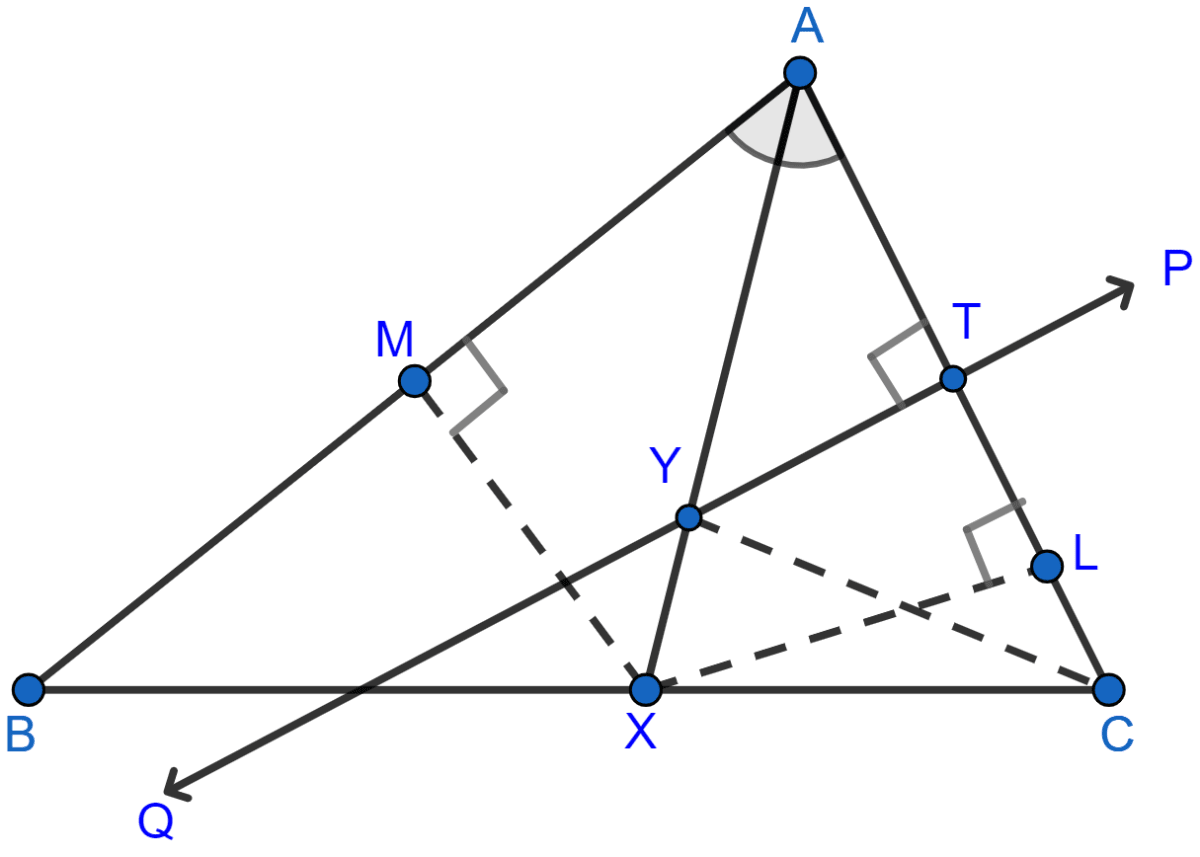
(i) In ∆AXL and ∆AXM,
⇒ ∠XAL = ∠XAM [Since, AX bisects angle BAC]
⇒ AX = AX [Common]
⇒ ∠XLA = ∠XMA [Each 90°]
∴ ∆AXL ≅ ∆AXM by AAS axiom.
∴ XL = XM [By C.P.C.T.]
Hence, proved that X is equidistant from AC and AB.
(ii) In ∆YTA and ∆YTC,
⇒ AT = CT [because PQ is perpendicular bisector of AC]
⇒ ∠YTA = ∠YTC [Each 90°]
⇒ YT = YT [Common]
∴ ∆YTA ≅ ∆YTC by SAS axiom.
∴ YA = YC [By C.P.C.T.]
Hence, proved that Y is equidistant from A and C.
Related Questions
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
In each of the given figures; PA = PB and QA = QB.
(i)
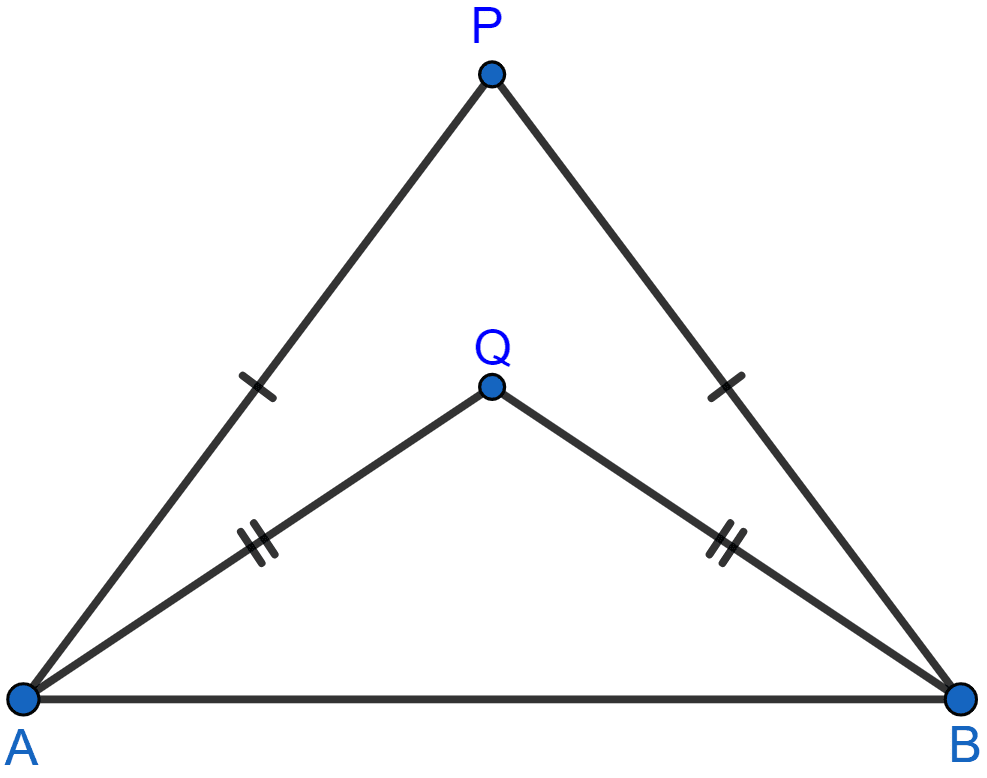
(ii)
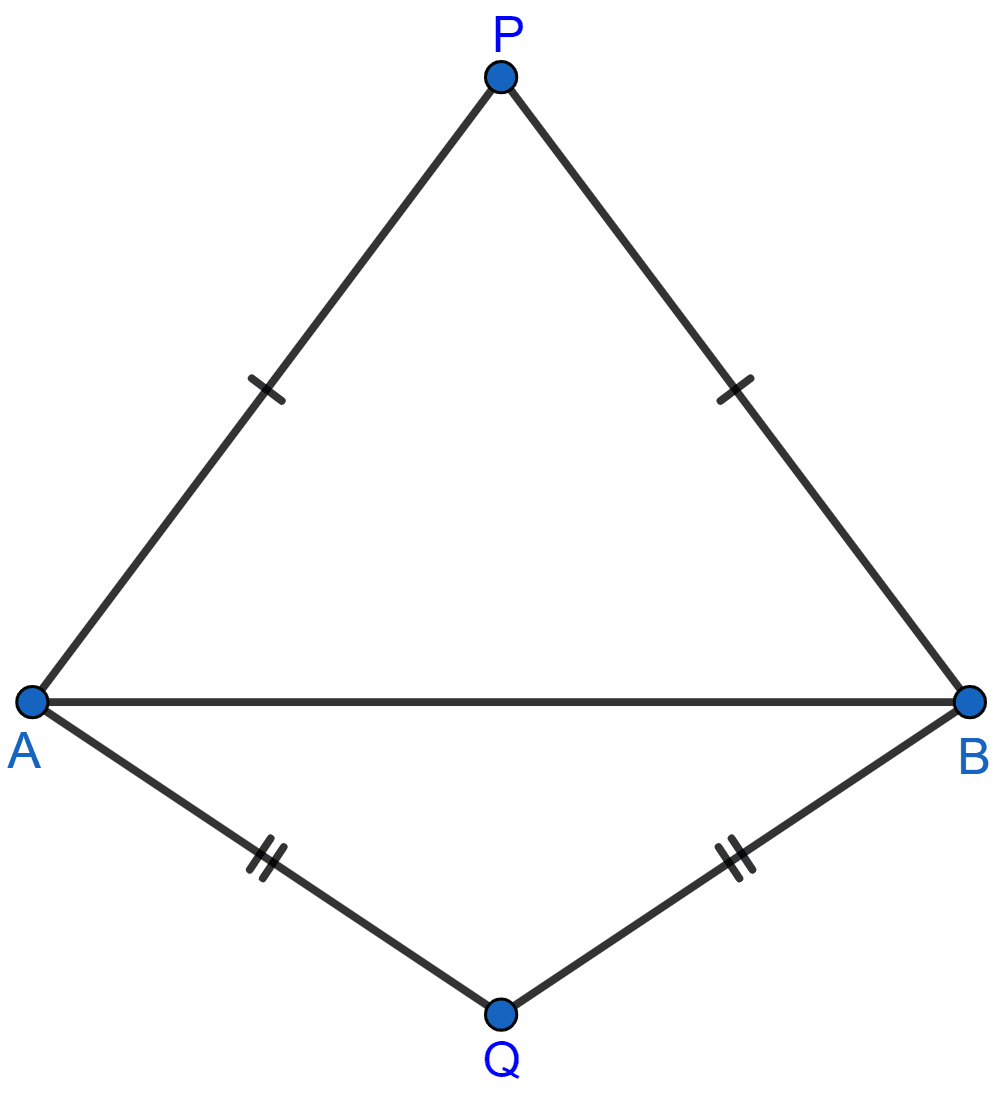
Prove in each case, that PQ (produce, if required) is perpendicular bisector of AB.
Hence, state the locus of the points equidistant from two given fixed points.
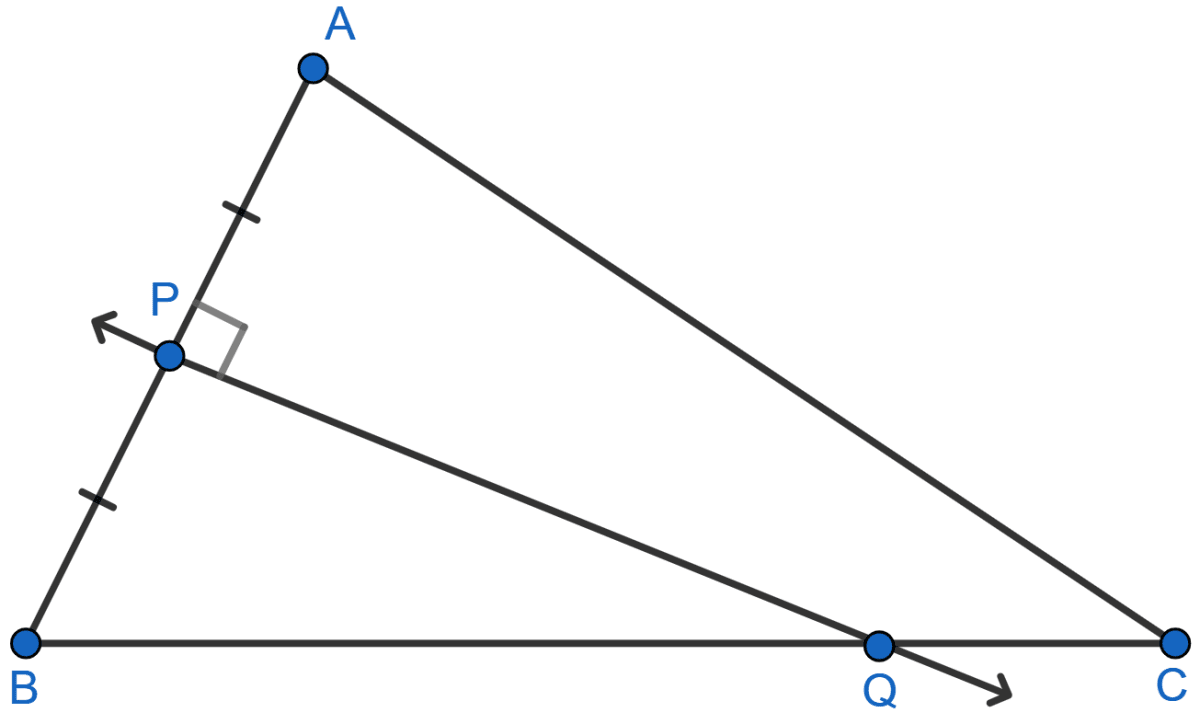
Given: CP is the bisector of angle C of ∆ABC.
Prove: P is equidistant from AC and BC.

Given: PQ is a perpendicular bisector of side AB of the triangle ABC.
Prove: Q is equidistant from A and B.