From the top of a cliff, the angles of depression of the top and bottom of a tower are observed to be 45° and 60° respectively. If the height of the tower is 20 m, find :

(i) the height of the cliff.

(ii) the distance between the cliff and the tower.

(i) Let AB be the cliff and CD be the tower.

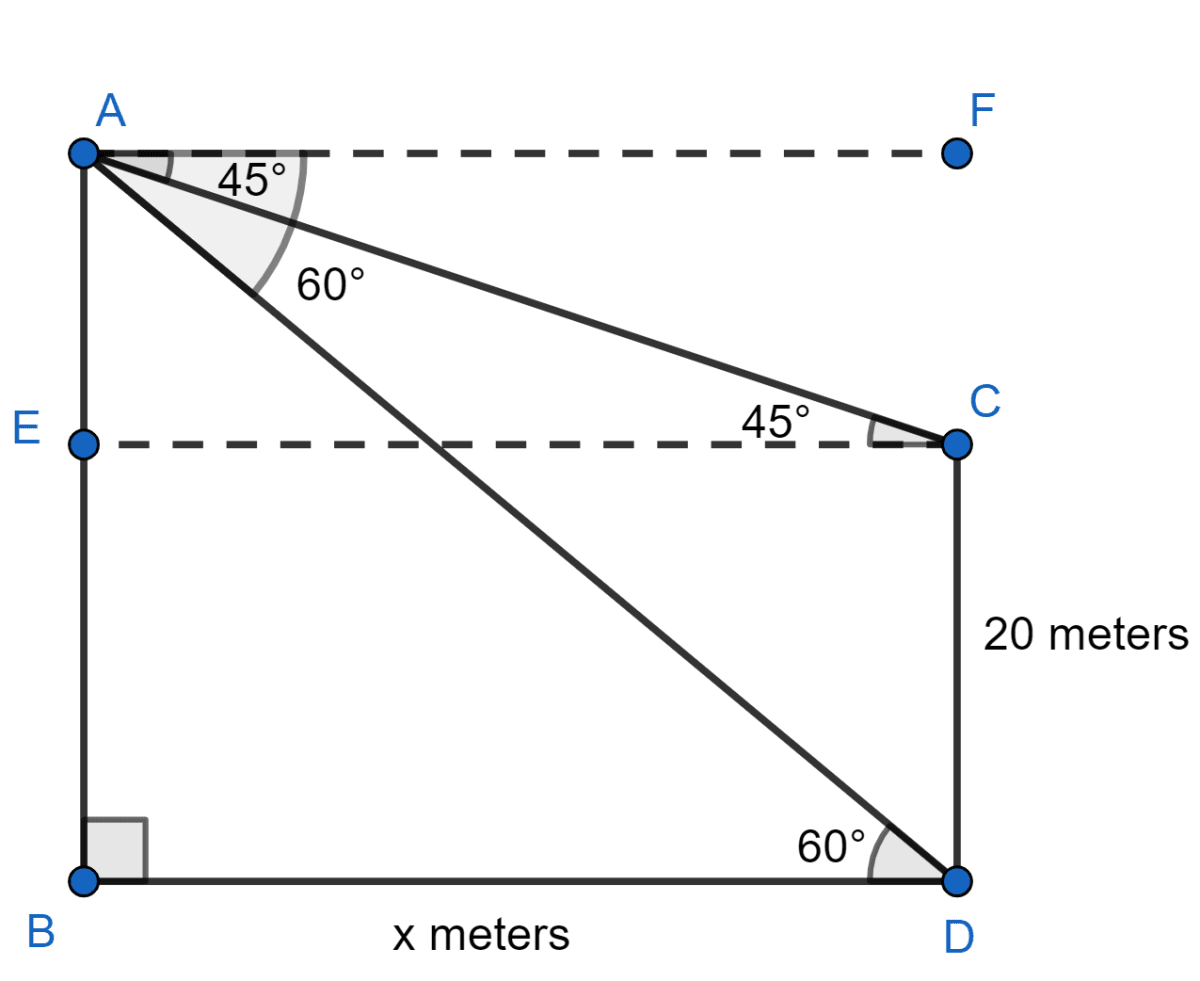
From figure,

∠ACE = ∠FAC = 45° (Alternate angles are equal)

∠ADB = ∠FAD = 60° (Alternate angles are equal)

Let BD = x.

From figure,

EC = BD = x meters.

EB = CD = 20 meters.

In △ AEC,

⇒ tan 45° = $\dfrac{AE}{EC}$

⇒ 1 = $\dfrac{AE}{x}$

⇒ AE = x meters.

In △ ABD,

$\Rightarrow \text{tan 60°} = \dfrac{AB}{BD} \\[1em] \Rightarrow \sqrt{3} = \dfrac{AE + EB}{x}\\[1em] \Rightarrow \sqrt{3} = \dfrac{x + 20}{x} \\[1em] \Rightarrow \sqrt{3}x = x + 20 \\[1em] \Rightarrow \sqrt{3}x - x = 20 \\[1em] \Rightarrow x(\sqrt{3} - 1) = 20 \\[1em] \Rightarrow x = \dfrac{20}{\sqrt{3} - 1} \\[1em] \Rightarrow x = \dfrac{20}{0.732} = 27.32 \text{ m}.$

From figure,

Height of cliff (AB) = AE + EB

= x + 20

= 27.32 + 20

= 47.32 meters.

Hence, the height of cliff = 47.32 meters.

(ii) From figure,

Distance between cliff and tower (BD) = x meters = 27.32 meters.

Hence, distance between cliff and tower = 27.32 meters.