Mathematics
From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate to the nearest metre, the distance of the buoy from the foot of the cliff.
Heights & Distances
104 Likes
Answer
Let MP be the cliff and O be the buoy.
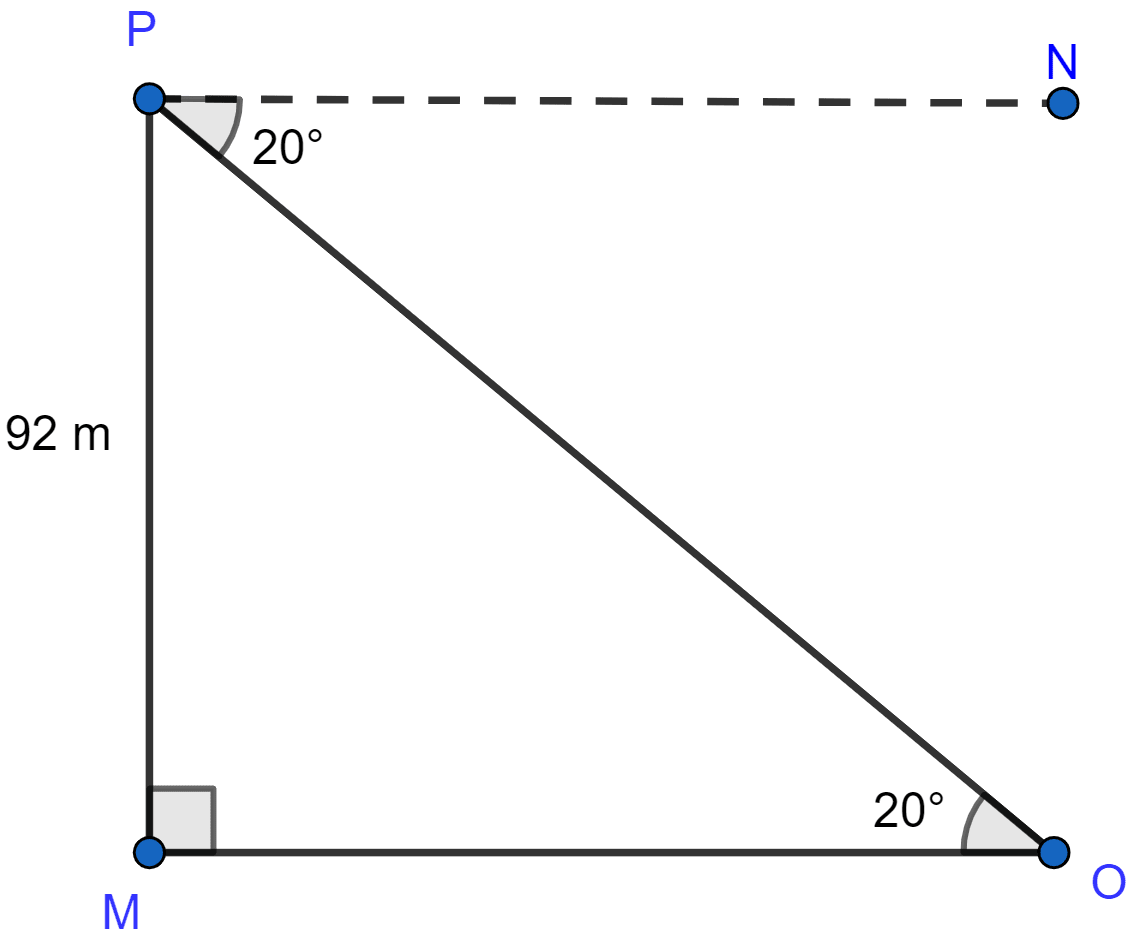
From figure,
Given angle of depression of a buoy is 20°.
∴ ∠POM = ∠OPN = 20° (Alternate angles are equal).
In △POM, ∠PMO = 90°.
From △POM, we get
Hence, the distance of buoy from the foot of cliff is 253 metres.
Answered By
37 Likes
Related Questions
What is the angle of elevation of sun when the length of shadow of a vertical pole is equal to its height?
From a point P on level ground, the angle of elevation of the top of a tower is 30°. If the tower is 100m high, how far is P from the foot of the tower ?
A boy is flying a kite with a string of length 100 m. If the string is tight and the angle of elevation of the kite is 26° 32', find the height of the kite correct to one decimal place (ignore the height of the boy).
An electric pole is 10 m high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.