From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm².

Given,

Diameter of solid cylinder (d) = 1.4 cm

Radius of solid cylinder (r) = $\dfrac{d}{2} = \dfrac{1.4}{2}$ = 0.7 cm.

Height of cylinder (h) = 2.4 cm

Height of conical cavity = Height of cylinder = h = 2.4 cm.

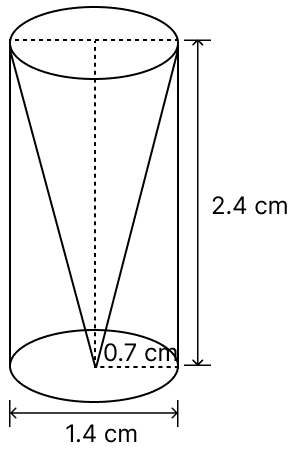
From figure,

Radius of conical cavity = Radius of cylinder = r = 0.7 cm.

By formula,

Slant height of cone (l) = $\sqrt{r^2 + h^2}$

Substituting value we get :

$l = \sqrt{(0.7)^2 + (2.4)^2} \\[1em] = \sqrt{0.49 + 5.76} \\[1em] = \sqrt{6.25} \\[1em] = 2.5 \text{ cm}.$

Total surface area of remaining solid = Curved surface area of cylinder + Curved surface area of cone + Base area of cylindrical portion

Substituting values we get :

Total surface area of remaining solid = 2πrh + πrl + πr²

= πr(2h + l + r)

= $\dfrac{22}{7}$ x 0.7 x (2 x 2.4 + 2.5 + 0.7)

= 22 x 0.1 x (4.8 + 2.5 + 0.7)

= 2.2 x 8

= 17.6 ≈ 18 cm²

Hence, the total surface area of the remaining solid = 18 cm².