The fourth vertex of a parallelogram ABCD, where A = (3, -2), B = (7, 6) and C = (3, 8) is :

1. D = (1, 0)

2. D = (-1, 0)

3. D = (0, 1)

4. D = (0, -1)

Let co-ordinates of D be (x, y).

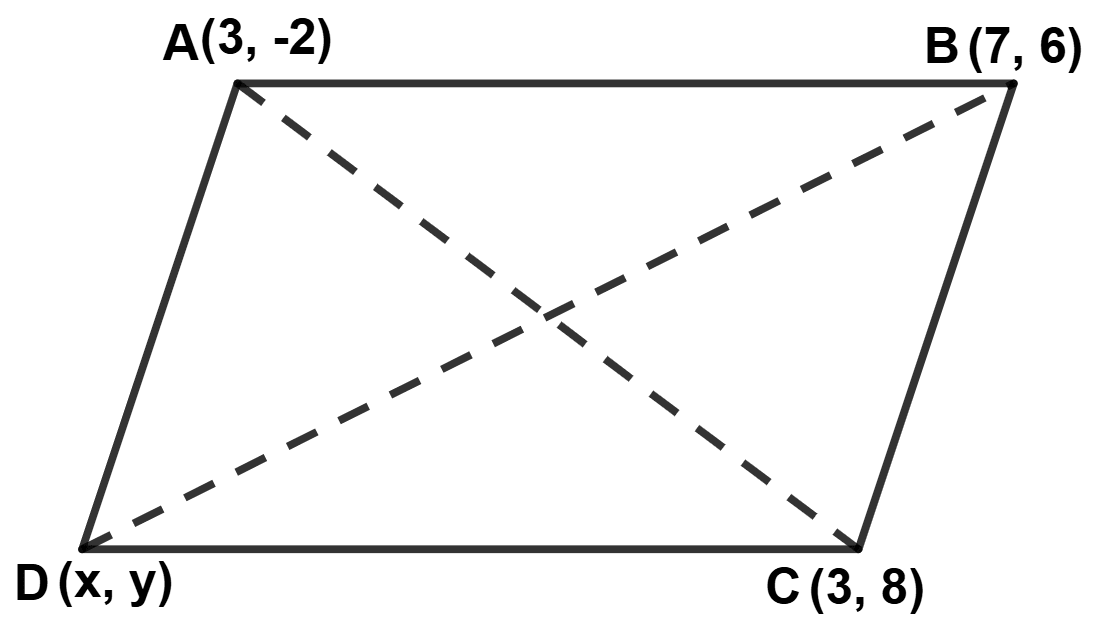
We know that,

Diagonals of parallelogram bisect each other.

∴ Mid-point of AC = Mid-point of BD.

$\therefore \Big(\dfrac{3 + 3}{2}, \dfrac{(-2) + 8}{2}\Big) = \Big(\dfrac{7 + x}{2}, \dfrac{6 + y}{2}\Big) \\[1em] \Rightarrow \Big(\dfrac{6}{2}, \dfrac{6}{2}\Big) = \Big(\dfrac{7 + x}{2}, \dfrac{6 + y}{2}\Big) \\[1em] \Rightarrow (3, 3) = \Big(\dfrac{7 + x}{2}, \dfrac{6 + y}{2}\Big) \\[1em] \Rightarrow \dfrac{7 + x}{2} = 3 \text{ and } \dfrac{6 + y}{2} = 3 \\[1em] \Rightarrow 7 + x = 6 \text{ and } 6 + y = 6 \\[1em] \Rightarrow x = 6 - 7 \text{ and } y = 6 - 6 \\[1em] \Rightarrow x = -1 \text{ and } y = 0.$

D = (x, y) = (-1, 0).

Hence, Option 2 is the correct option.