Mathematics

Foot of a 10 m long ladder leaning against a vertical well is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.

Pythagoras Theorem

16 Likes

Answer

Let AB be the ladder and BC be the vertical well.

So, △ABC is right triangle.

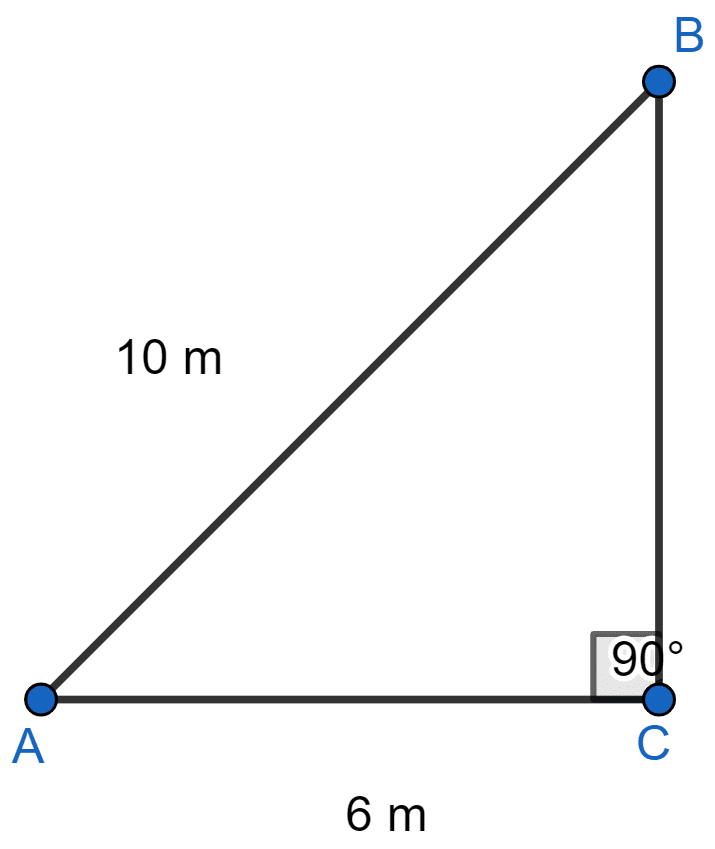
Foot of a 10 m long ladder leaning against a vertical well is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches. Pythagoras Theorem, ML Aggarwal Understanding Mathematics Solutions ICSE Class 9.

By pythagoras theorem,

⇒ AB² = BC² + AC²

⇒ 10² = BC² + (6)²

⇒ 100 = BC² + 36

⇒ BC² = 100 - 36 = 64

⇒ BC = $\sqrt{64}$ = 8 m.

Hence, the top of the ladder reaches 8 m above the wall of well.

Answered By

10 Likes

Related Questions

A guy attached a wire 24 m long to a vertical pole of height 18 m and has a stake attached to other end. How far from the base of the pole should the stake be driven so that the wire will be taught ?
View Answer