Mathematics
Find the value of k such that the line (k – 2)x + (k + 3)y – 5 = 0 is:
(i) perpendicular to the line 2x – y + 7 = 0
(ii) parallel to it.
Straight Line Eq
7 Likes
Answer
Given line equation,
⇒ 2x - y + 7 = 0 ……….(1)
⇒ y = 2x + 7
Comparing above equation with y = mx + c we get,
Slope (m1) = 2
Given line equation,
⇒ (k - 2)x + (k + 3)y - 5 = 0 ……….(2)
⇒ (k + 3)y = -(k - 2)x + 5
⇒ y =
Comparing above equation with y = mx + c we get,
Slope (m2) =
(i) If lines (1) and (2) are perpendicular then product of their slopes = -1.
⇒ m1 x m2 = -1
Hence, k = 7.
(ii) If lines 1 and 2 are parallel then their slopes will be equal.
⇒ = 2
⇒ -(k - 2) = 2(k + 3)
⇒ -k + 2 = 2k + 6
⇒ 2k + k = 2 - 6
⇒ 3k = -4
⇒ k = .
Hence, k = .
Answered By
4 Likes
Related Questions
The vertices of a triangle ABC are A (0, 5), B (-1, -2) and C (11, 7). Write down the equation of BC. Find :
(i) the equation of line through A and perpendicular to BC.
(ii) the co-ordinates of the point P, where the perpendicular through A, as obtained in (i), meets BC.
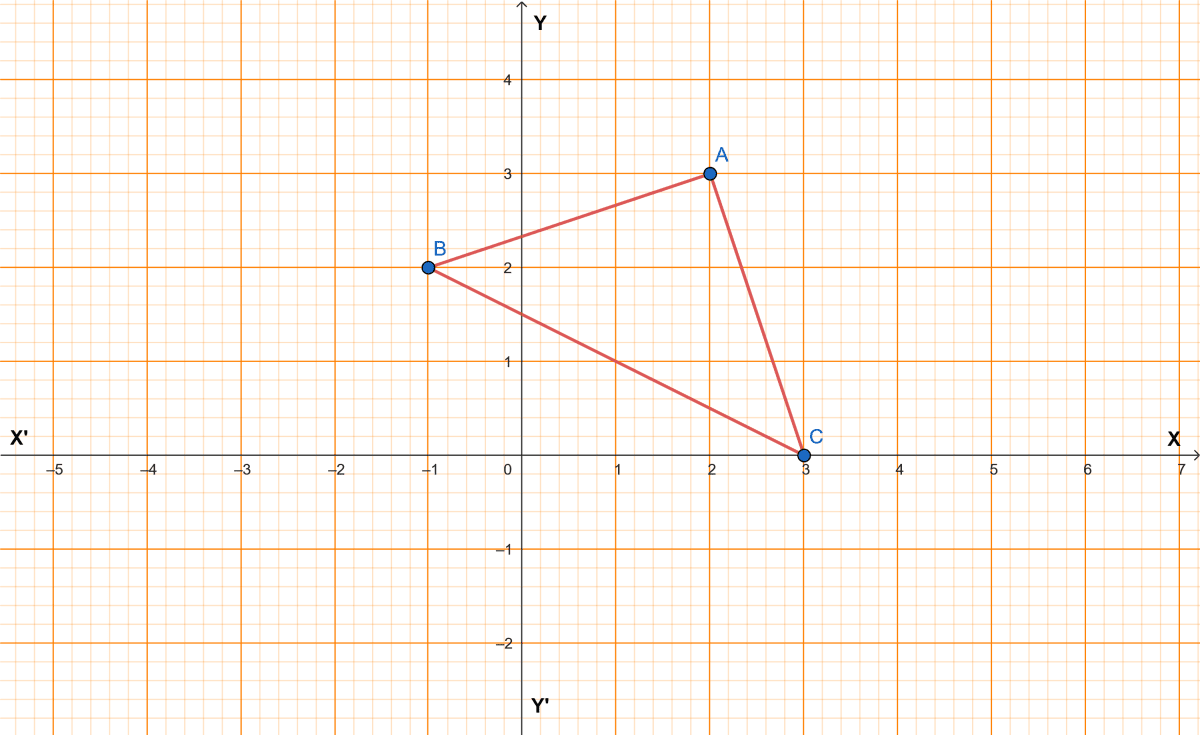
From the given figure, find:
(i) the co-ordinates of A, B and C.
(ii) the equation of the line through A and parallel to BC.
Determine whether the line through points (-2, 3) and (4, 1) is perpendicular to the line 3x = y + 1.
Does the line 3x = y + 1 bisect the line segment joining the two given points?
Given a straight line x cos 30° + y sin 30° = 2. Determine the equation of the other line which is parallel to it and passes through (4, 3).