Find the radius of a circle if a 90° arc has a length of 3.5π cm. Hence, find the area of the sector formed by this arc.

From figure,

AOB is a quadrant, with ∠AOB = 90°.

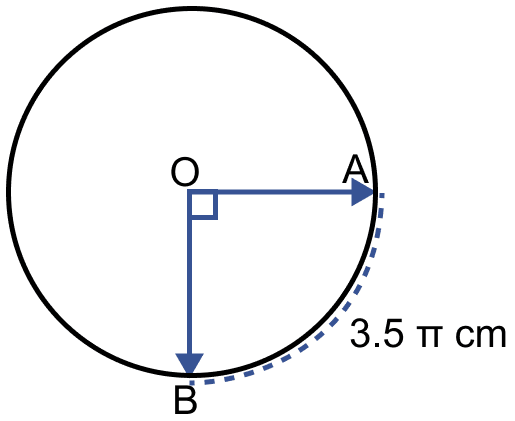
Let radius of circle be r cm,

Circumference of quadrant = $\dfrac{2πr}{4} = \dfrac{πr}{2}$.

Given,

Circumference of quadrant = 3.5π

$\Rightarrow \dfrac{πr}{2} = 3.5 π \\[1em] \Rightarrow \dfrac{r}{2} = 3.5 \\[1em] \Rightarrow r = 7 \text{ cm}.$

Area of sector = $πr^2 \times \dfrac{90°}{360°}$

$= \dfrac{22}{7} \times 7^2 \times \dfrac{1}{4} \\[1em] = 22 \times 7 \times \dfrac{1}{4} \\[1em] = \dfrac{154}{4} \\[1em] = 38.5 \text{ cm}^2.$

Hence, radius = 7 cm and area of sector = 38.5 cm².