Mathematics
Find the image of the point (1, 2) in the line x - 2y - 7 = 0.
Straight Line Eq
135 Likes
Answer
The given line is x - 2y - 7 = 0 …..(i)
⇒ 2y = x - 7
⇒ y = .
The slope of the line (i) = m1 =
Let the point (1, 2) be P.
From P draw a perpendicular to the line (i) and produce it to point P' such that P'M = MP, then P' is the image of P in line (i) and line (i) is the right bisector of the segment PP'.
Let P' be (a, b).
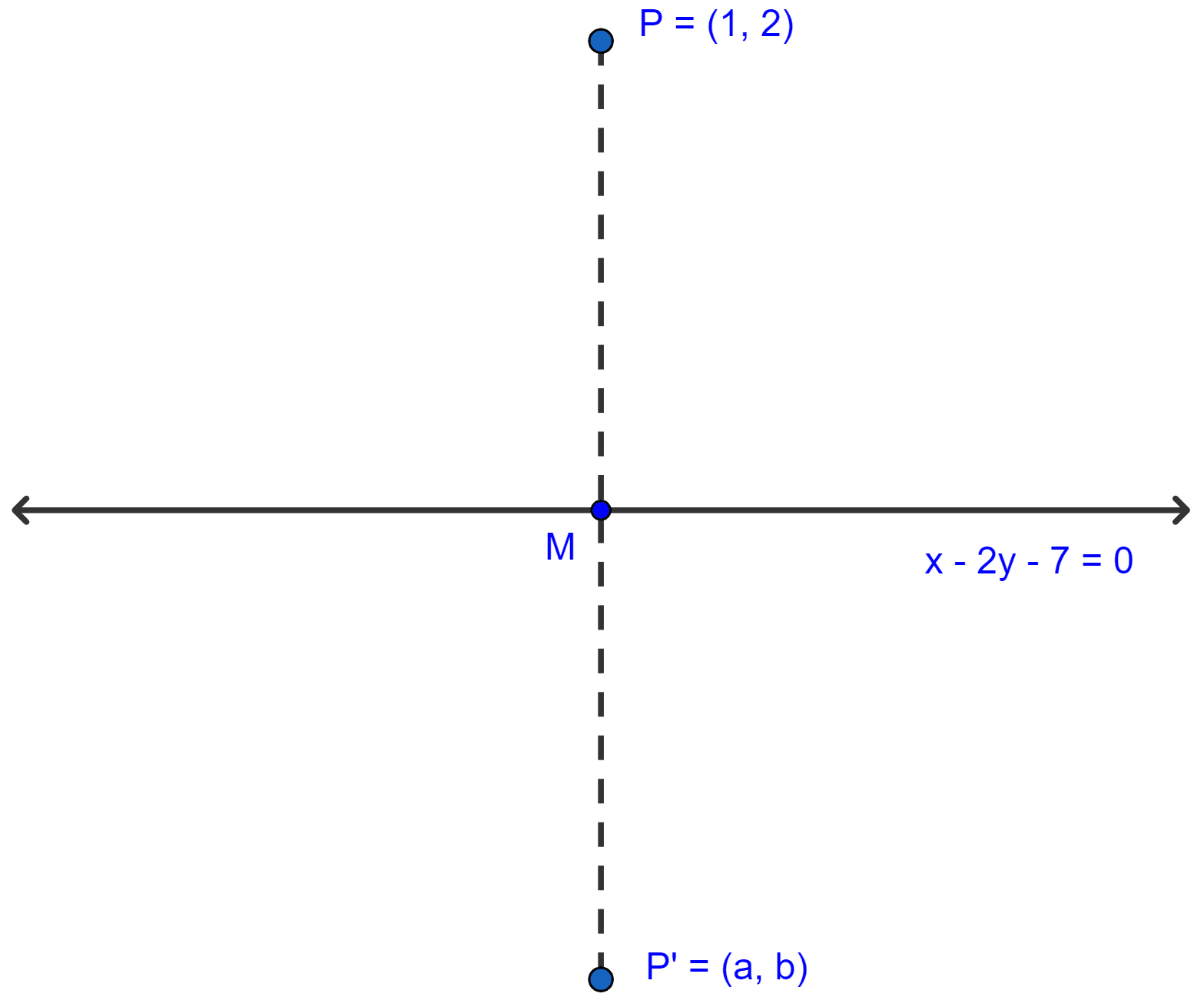
Then slope of PP' = m2 = .
Since, line (i) is perpendicular to PP' so,
Also mid-point of PP' is M.
Since, (i) is the right bisector of the segment PP', M lies on (i)
Multiplying equation (iv) by 2 and subtracting from (iii) we get,
Putting value of b in Eq (iii),
⇒ 2a - 6 = 4
⇒ 2a = 10
⇒ a = 5.
P' = (a, b) = (5, -6).
Hence, the coordinates of image are (5, -6).
Answered By
25 Likes
Related Questions
The points B(1, 3) and D(6, 8) are two opposite vertices of a square ABCD. Find the equation of the diagonal AC.
ABCD is a rhombus. The coordinates of A and C are (3, 6) and (-1, 2) respectively. Write down the equation of BD.
If the line x - 4y - 6 = 0 is the perpendicular bisector of the line segment PQ and the coordinates of P are (1, 3), find the coordinates of Q.
OABC is a square, O is the origin and the points A and B are (3, 0) and (p, q). If OABC lies in the first quadrant, find the values of p and q. Also write down the equations of AB and BC.