Find the equations of the diagonals of a rectangle whose sides are x = -1, x = 2, y = -2 and y = 6.

These lines x = -1, x = 2, y = -2 and y = 6 form a rectangle when they intersect at A, B, C and D.

From graph we get coordinates of A, B, C and D as (-1, -2), (2, -2), (2, 6) and (-1, 6) respectively.

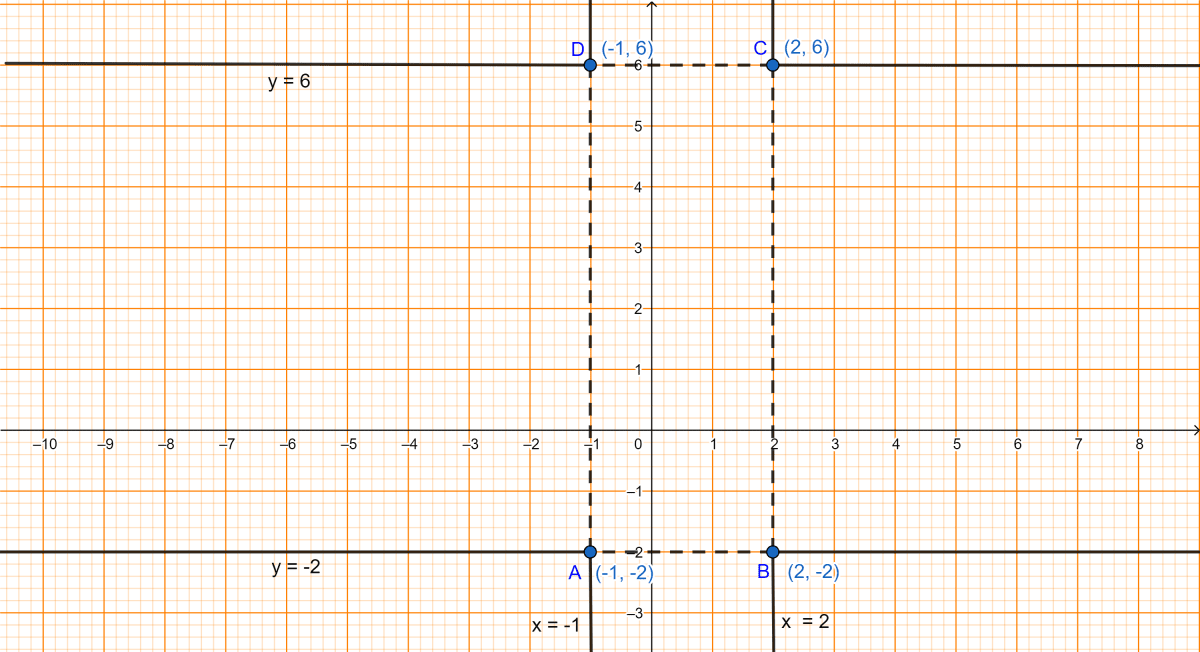
Equation of AC can be given by two point formula i.e.,

$\Rightarrow y - y$1 = \dfrac{y2 - y1}{x2 - x1}(x - x1) \\[1em] \Rightarrow y - (-2) = \dfrac{6 - (-2)}{2 - (-1)}(x - (-1)) \\[1em] \Rightarrow y + 2 = \dfrac{8}{3}(x + 1) \\[1em] \Rightarrow 3(y + 2) = 8(x + 1) \\[1em] \Rightarrow 3y + 6 = 8x + 8 \\[1em] \Rightarrow 8x - 3y + 2 = 0.

Equation of BD can also be given by two point formula i.e.,

$\Rightarrow y - y$1 = \dfrac{y2 - y1}{x2 - x1}(x - x1) \\[1em] \Rightarrow y - (-2) = \dfrac{6 - (-2)}{-1 - 2}(x - 2) \\[1em] \Rightarrow y + 2 = \dfrac{8}{-3}(x - 2) \\[1em] \Rightarrow -3(y + 2) = 8(x - 2) \\[1em] \Rightarrow -3y - 6 = 8x - 16 \\[1em] \Rightarrow 8x + 3y - 10 = 0.

Hence, the equations of the diagonals of the rectangle are 8x - 3y + 2 = 0 and 8x + 3y - 10 = 0.