Mathematics
E and F are points on the sides PQ and PR respectively of a △PQR. For each of the following cases, state whether EF || QR :
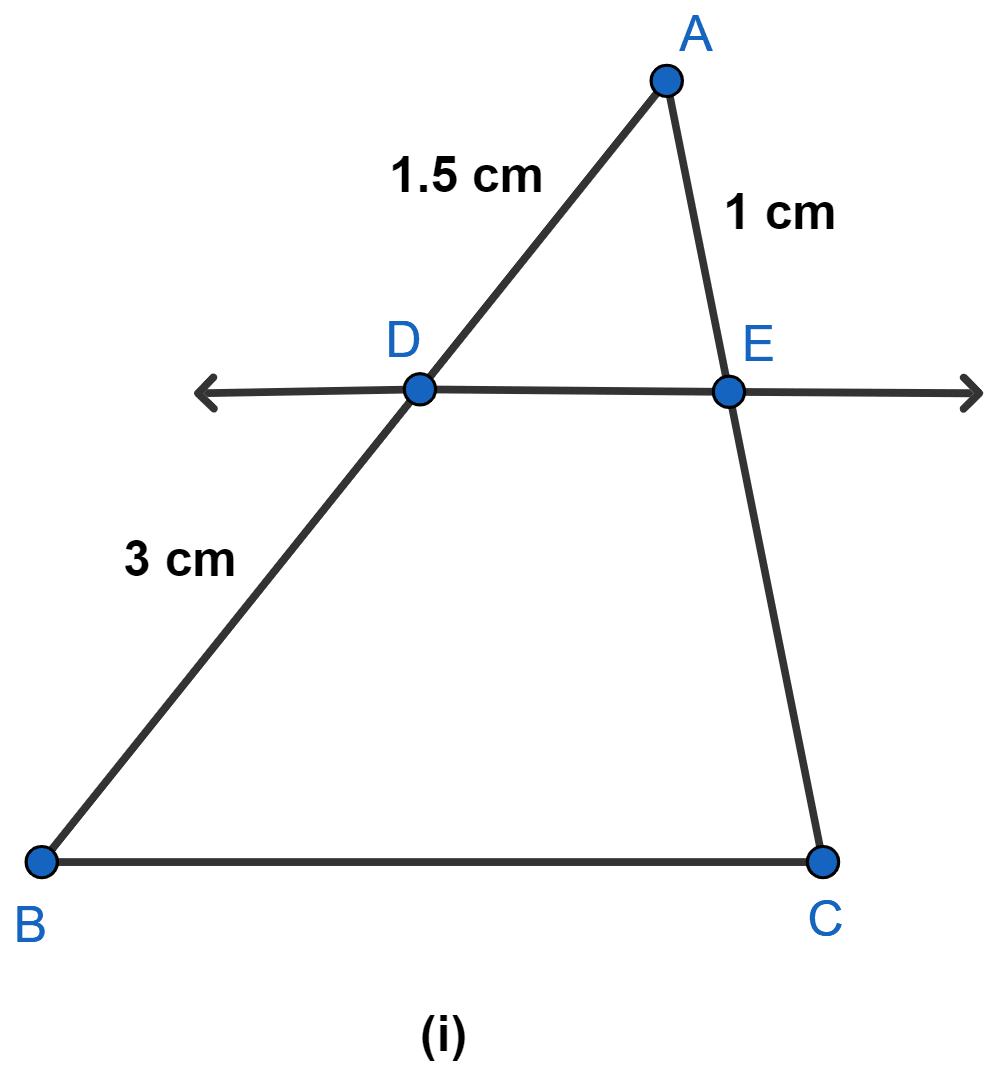
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
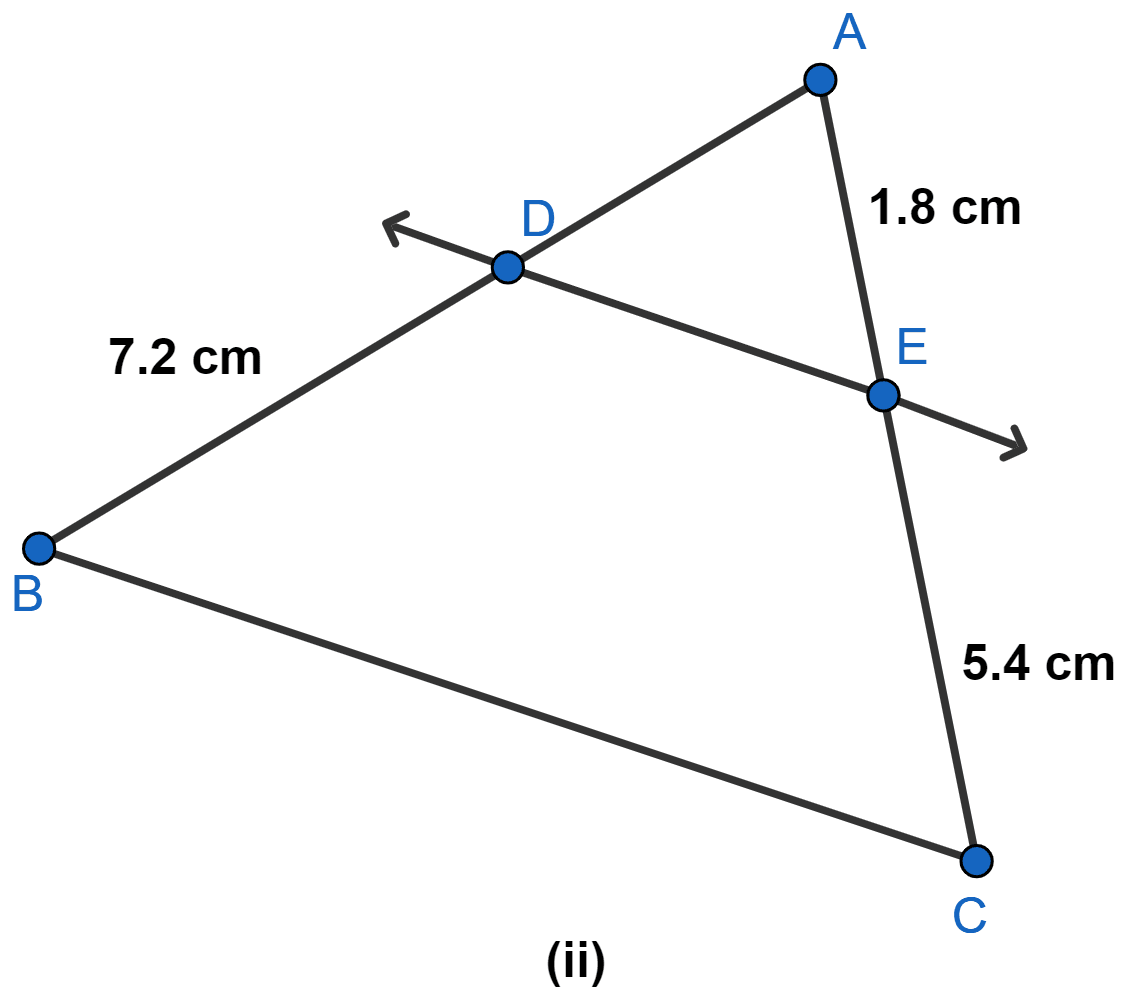
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Triangles
1 Like
Answer
We know that,
If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
∴ EF || QR if
………..(1)
(i) Given,
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm.

Substituting values in L.H.S. of equation (1), we get :
Substituting values in R.H.S. of equation (1), we get :
Since, .
Hence, in this case EF is not parallel to QR.
(ii) Given,
PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm.
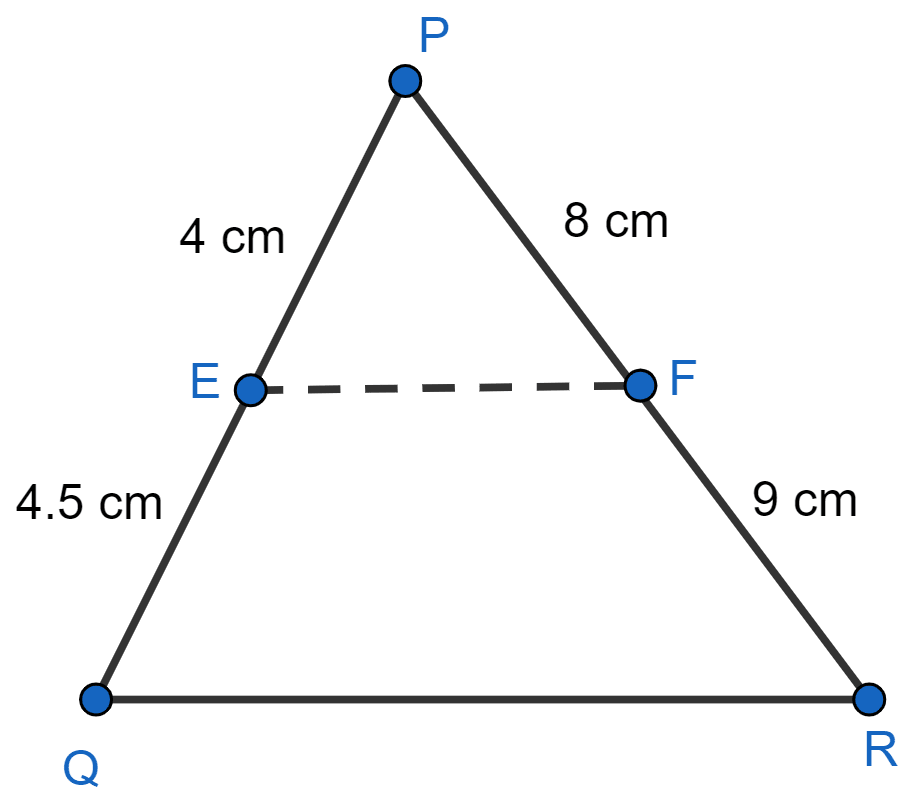
Substituting values in L.H.S. of equation (1), we get :
Substituting values in R.H.S. of equation (1), we get :
Since, .
Hence, in this case EF is parallel to QR.
(iii) Given,
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm.
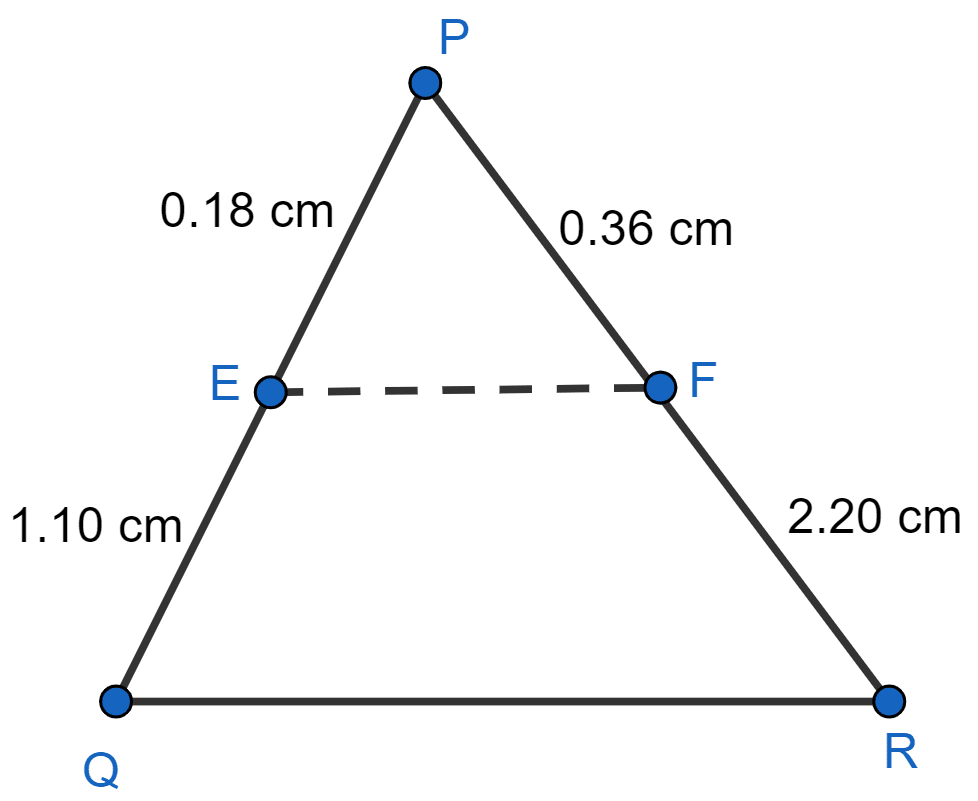
From figure,
⇒ EQ = PQ - PE = 1.28 - 0.18 = 1.10 cm
⇒ FR = PR - PF = 2.56 - 0.36 = 2.20 cm
Substituting values in L.H.S. of equation (1), we get :
Substituting values in R.H.S. of equation (1), we get :
Since, .
Hence, in this case EF is parallel to QR.
Answered By
2 Likes