Mathematics
Draw and describe the locus of vertices of all isosceles triangles having a common base.
Locus
20 Likes
Answer
△ABC is an isosceles triangle in which AB = AC.
From A, draw AD perpendicular to BC.
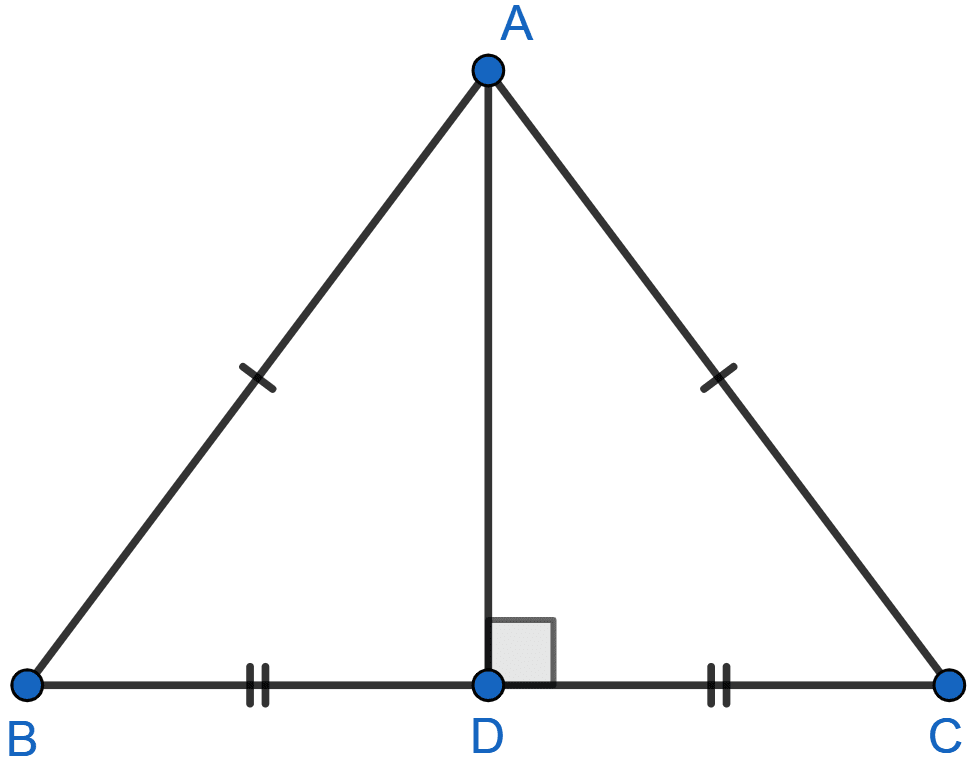
In △ABD and △ACD
AD = AD (Common sides)
AB = AC (Since, triangle is isosceles)
∠ADB = ∠ADC (90°)
Hence, by SAS axiom △ABD ~ △ACD. Since, triangles are similar so the ratio of the corresponding sides will be equal,
Since, BD = DC so AD can be said as the perpendicular bisector of BC.
Hence, the locus of vertices will be the perpendicular bisector of the base.
Answered By
15 Likes
Related Questions
A, B are fixed points. State the locus of P so that ∠APB = 60°.
Draw and describe the locus of points at a distance 2.5 cm from the fixed line.
Draw and describe the locus of points inside a circle and equidistant from two fixed points on the circle.
Draw and describe the locus of centres of all circles passing through two fixed points.