Draw and describe the locus of a point in rhombus ABCD which is equidistant from AB and AD.

Let ABCD be a rhombus.

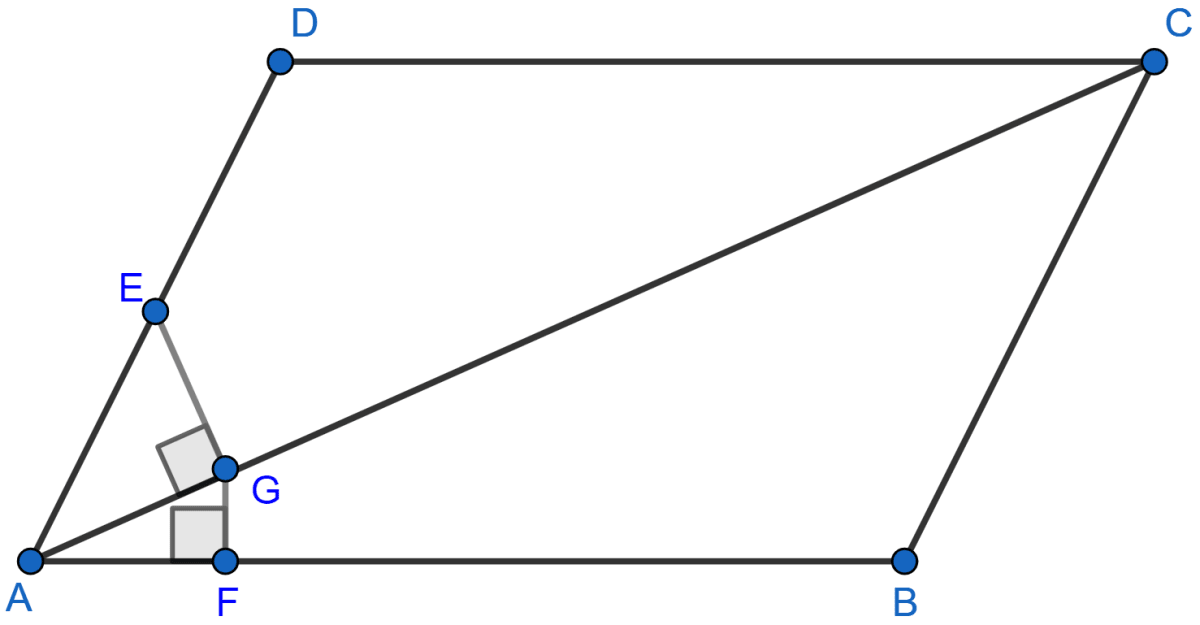
AC is diagonal of rhombus which will bisect angle A. As rhombus bisects the vertices angle.

∴ AC bisects ∠A

Let there be a point E and F on the sides AD and AB respectively. Draw a line perpendicular to AC from both the points.

Considering △AEG and △AFG

∠AGE = ∠AFG (Both are equal to 90°)
∠EAG = ∠FAG (Both are equal to half of ∠DAB.)

Hence, by AA axiom △AEG ~ △AFG.

Since triangles are similar so the ratio of their corresponding sides will be similar.

$\therefore \dfrac{EG}{FG} = \dfrac{AG}{AG} \\[1em] \Rightarrow \dfrac{EG}{FG} = 1 \\[1em] \Rightarrow EG = FG.$

Since, distance from AD and AB is similar,

Hence, the locus of point is the diagonal AC of the rhombus ABCD.