Draw a diagram of combination of three movable pulleys and one fixed pulley to lift up a load. In the diagram, show the directions of load, effort and tension in each strand. Find:

(i) the mechanical advantage,

(ii) velocity ratio and

(iii) the efficiency of the combination in the ideal situation.

The diagram is shown below:

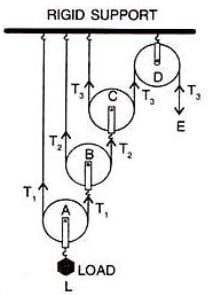
In equilibrium,

Effort E = T₃       (1)

Tension T₁ in the string passing over the pulley A is given as 2T₁ = L

T₁ = $\bold{\dfrac{L}{2}}$       (2)

Tension T₂ in the string passing over the pulley B is given as

2T₂ = T₁

T₂= $\dfrac{T_1}{2}$

Substituting value of T₁ from equation 2,

T₂ = $\bold{\dfrac{L}{2^2}}$       (3)

Tension T₃ in the string passing over the pulley C is given as

2T₃ = T₂

T₃ = $\dfrac{T_2}{2}$

Substituting value of T₂ from equation 3,

T₃ = $\bold{\dfrac{L}{2^3}}$       (4)

In equilibrium, T₃ = E

From equation 4,

Load L = 2³ x T₃       (5)

$\text{Mechanical advantage M.A.} = \dfrac{L}{E} \\[0.5em] M.A. = \dfrac{2^3 \times T_3}{T^3} \\[0.5em] \Rightarrow M.A. = 2^3$

(ii) As we know, one end of each string passing over a movable pulley is fixed, so the other end of string moves up twice the distance moved by the axle of the movable pulley.

If the load L attached to the pulley A moves a distance d,

then d_L = d

Now, the string connected to the axle of pulley B, moves up by a distance,

2 times d = 2d.

Then the string connected to the axle of the pulley C, moves up by a distance,

2 times 2d = 2²d

Then the end of the string passing over the fixed pulley D, moves up by a distance,

2 times 2²d = 2³d.

Hence, d_E = 2³d.

As we know,

$\text{Velocity Ratio V.R.} = \dfrac{\text{Distance moved by effort }}{\text{Distance moved by load}} \\[0.5em] = \dfrac{d$E}{dL} \\[0.5em]

Substituting the values in the formula we get,

$= \dfrac {2^3 \times d}{d} \\[0.5em] = 2^3 \\[1.5em] \text{Efficiency} (\eta) = \dfrac{M.A.}{V.R.} \\[0.5em] = \dfrac{2^3}{2^3} = 1 \\[0.5em]$