Mathematics

Draw a cumulative frequency curve (ogive) for the following distributions :
Class interval Frequency
10 - 19 23
20 - 29 16
30 - 39 15
40 - 49 20
50 - 59 12

14 Likes

The above distribution is discontinuous converting into continuous distribution, we get :

Adjustment factor = (Lower limit of one class - Upper limit of previous class) / 2

= $\dfrac{20 - 19}{2} = \dfrac{1}{2}$

= 0.5

Subtract the adjustment factor (0.5) from all the lower limits and add the adjustment factor (0.5) to all the upper limits.

Classes before adjustment	Classes after adjustment	Frequency	Cumulative frequency
10 - 19	9.5 - 19.5	23	23
20 - 29	19.5 - 29.5	16	39 (23 + 16)
30 - 39	29.5 - 39.5	15	54 (39 + 15)
40 - 49	39.5 - 49.5	20	74 (54 + 20)
50 - 59	49.5 - 59.5	12	86 (74 + 12)

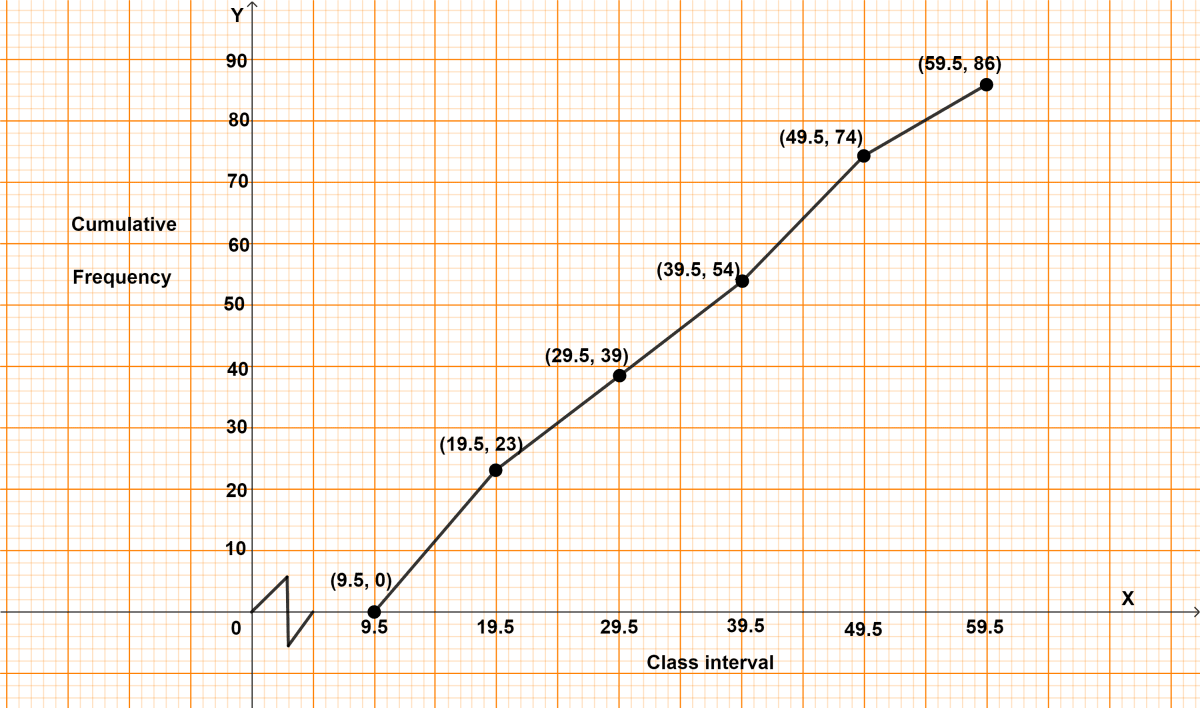
Steps of construction of ogive :

Since, the scale on x-axis starts at 9.5, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 9.5.
Take 2 cm = 10 units along x-axis.
Take 1 cm = 10 units along y-axis.
Ogive always starts from a point on x-axis representing the lower limit of the first class. Mark point (9.5, 0).
Take upper class limits along x-axis and corresponding cumulative frequencies along y-axis, mark the points (19.5, 23), (29.5, 39), (39.5, 54), (49.5, 74) and (59.5, 86).
Join the points marked by a free hand curve.

The required ogive is shown in the below figure:

Answered By

10 Likes