Mathematics
Determine the ratio in which the line y = 2 + 3x divides the line segment AB joining the points A(-3, 9) and B(4, 2).
Section Formula
16 Likes
Answer
By two point form,
Equation of line :
⇒ y - y1 = (x - x1)
Equation of AB :
Solving equation y = 2 + 3x and x + y = 6 simultaneously,
⇒ x + y = 6 …….(1)
⇒ y = 2 + 3x …….(2)
Substituting value of y from equation (2) in (1), we get :
⇒ x + (2 + 3x) = 6
⇒ 4x + 2 = 6
⇒ 4x = 6 - 2
⇒ 4x = 4
⇒ x =
⇒ x = 1.
Substituting value of x in equation (2), we get :
⇒ y = 2 + 3(1) = 2 + 3 = 5.
Let (1, 5) divide the line AB in the ratio k : 1.
By section formula,
(x, y) =
Substituting values we get :
Hence, the line y = 2 + 3x divides the line segment AB in the ratio 4 : 3.
Answered By
9 Likes
Related Questions
Write the first five terms of the sequence given by , n ∈ N.
(a) Is the sequence an A.P. or G.P.?
(b) If the sum of its first ten terms is , find the value of p.
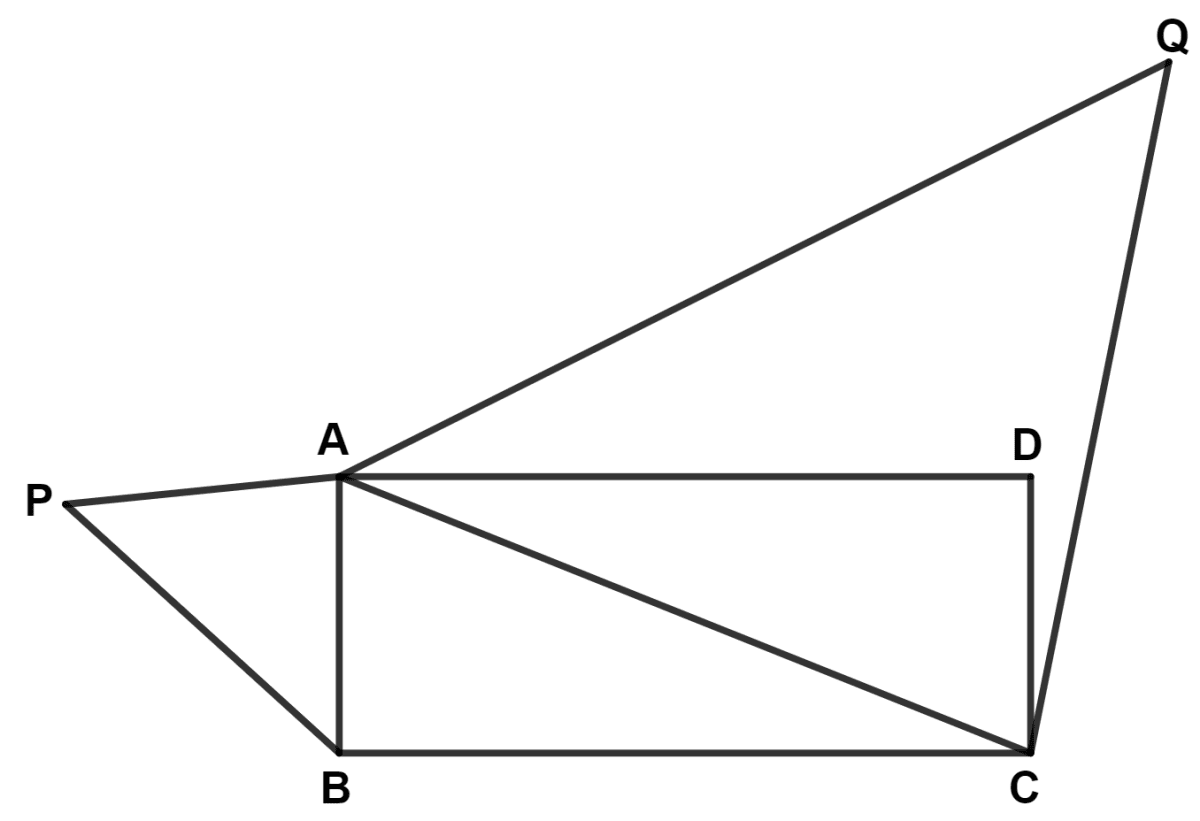
ABCD is a rectangle where side BC is twice side AB. If △ACQ ~ △BAP, find area of △BAP : area of △ACQ.
Square ABCD lies in the third quadrant of a XY plane such that its vertex A is at (-3, -1) and the diagonal DB produced is equally inclined to both the axes. The diagonals AC and BD meets at P(-2, -2). Find the :
(a) Slope of BD
(b) equation of AC
ABC is a triangle as shown in the figure below.
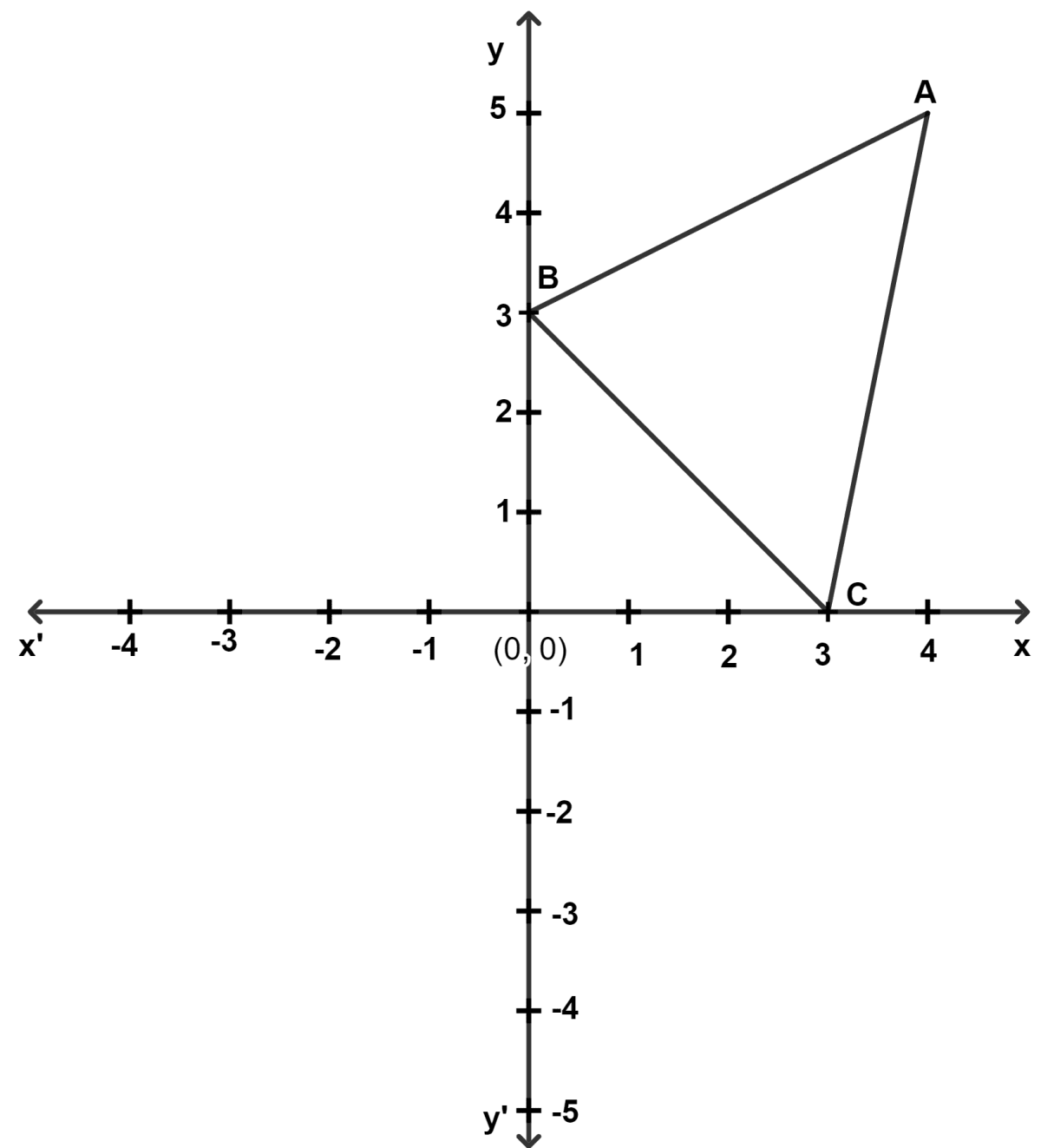
(a) Write down the coordinates of A, B and C on reflecting through the origin.
(b) Write down the coordinates of the point/s which remain invariant on reflecting the triangle ABC on the x-axis and y-axis respectively.