Describe completely the locus of centre of a circle of varying radius and touching two arms of ∠ABC.

Let there be two circles with centre O and O' and BD be the angle bisector of ∠ABC.

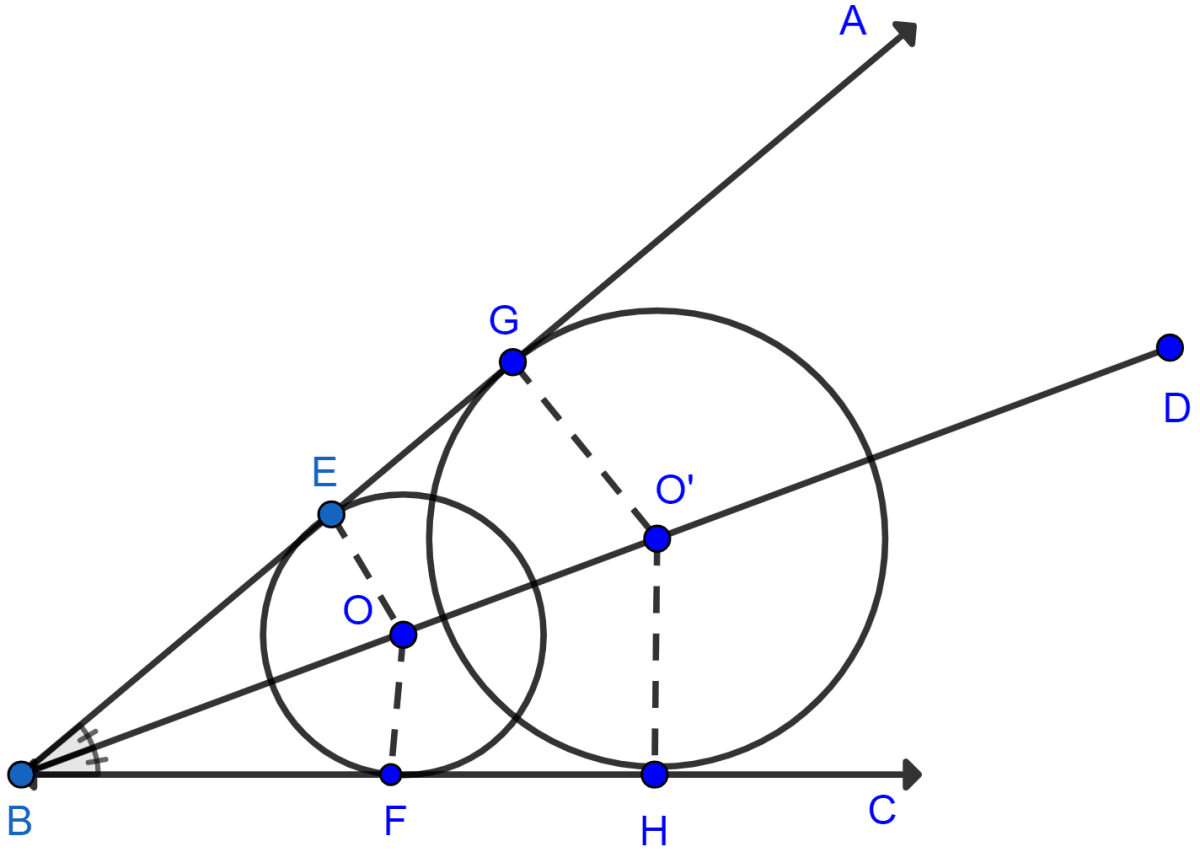
AB and BC are two tangents to the circle.

We know that radius and tangent make 90°.

From graph,

∠OEB = ∠OFB (Both are equal to 90)

∠OBE = ∠OBF (Since, BX is the angle bisector of ∠ABC.)

Hence, by AA axiom △OEB ~ △OFB.

Since triangles are similar hence, the ratio of their corresponding sides are similar.

$\therefore \dfrac{OE}{OB} = \dfrac{OF}{OB} \\[1em] \Rightarrow OE = \dfrac{OF}{OB} \times OB \\[1em] \Rightarrow OE = OF \\[1em]$

Since, O is the centre hence, we can say that OE = OF = radius. Thus circle with centre O is at equal distance from both arms of angle.

Similarly,

From graph,

∠O'GB = ∠O'HB (Both are equal to 90)

∠O'BG = ∠O'BH (Since, BX is the angle bisector of ∠ABC.)

Hence, by AA axiom △O'GB ~ △O'HB.

Since triangles are similar hence, the ratio of their corresponding sides are similar.

$\therefore \dfrac{O'G}{O'B} = \dfrac{O'H}{O'B} \\[1em] \Rightarrow O'G = \dfrac{O'H}{O'B} \times O'B \\[1em] \Rightarrow O'G = O'H \\[1em]$

Since, O' is the centre hence, we can say that O'G = O'H = radius. Thus circle with centre O' is at equal distance from both arms of angle.

Hence, the locus is the bisector of the ∠ABC.