Mathematics
Describe completely the locus of centre of a circle of varying radius and touching two arms of ∠ABC.
Locus
12 Likes
Answer
Let there be two circles with centre O and O' and BD be the angle bisector of ∠ABC.
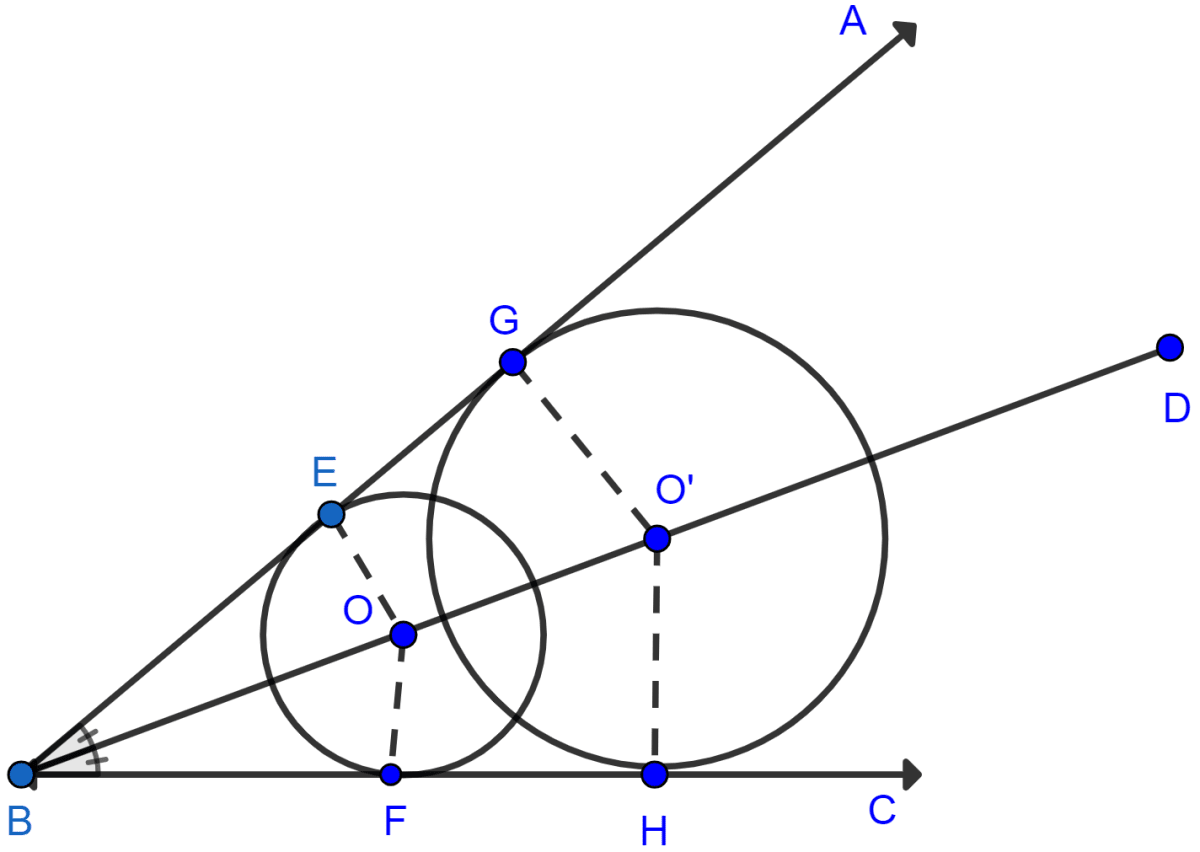
AB and BC are two tangents to the circle.
We know that radius and tangent make 90°.
From graph,
∠OEB = ∠OFB (Both are equal to 90)
∠OBE = ∠OBF (Since, BX is the angle bisector of ∠ABC.)
Hence, by AA axiom △OEB ~ △OFB.
Since triangles are similar hence, the ratio of their corresponding sides are similar.
Since, O is the centre hence, we can say that OE = OF = radius. Thus circle with centre O is at equal distance from both arms of angle.
Similarly,
From graph,
∠O'GB = ∠O'HB (Both are equal to 90)
∠O'BG = ∠O'BH (Since, BX is the angle bisector of ∠ABC.)
Hence, by AA axiom △O'GB ~ △O'HB.
Since triangles are similar hence, the ratio of their corresponding sides are similar.
Since, O' is the centre hence, we can say that O'G = O'H = radius. Thus circle with centre O' is at equal distance from both arms of angle.
Hence, the locus is the bisector of the ∠ABC.
Answered By
4 Likes
Related Questions
Describe completely the locus of point in a plane equidistant from a given line.
Describe completely the locus of point in a plane, at a constant distance of 5 cm from a fixed point (in the plane).
Describe completely the locus of centre of a circle of radius 2 cm and touching a fixed circle of radius 3 cm with centre O.
Using ruler and compasses, construct
(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.
(ii) the locus of points equidistant from A and C.