Derive an expression for equivalent resistance in the following case

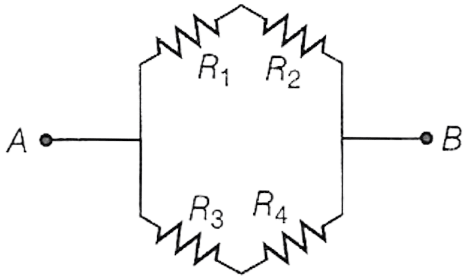
Decide, which resistances are in series and parallel. Solve for series and then for parallel. Combine both the results to get the equivalent resistance.

In the circuit, there are three parts. In the first part, resistors of R₁ and R₂ Ω are connected in series. If the equivalent resistance of this part is R'_s then

R'_s = R₁ + R₂

In the second part, resistors of R₃ and R₄ are connected in series. If the equivalent resistance of this part is R''_s then

R''_s = R₃ + R₄

In the third part, the two parts of resistance R'_s and R''_s are connected in parallel. If the equivalent resistance between points A and B is R_p then

$\dfrac{1}{R$p} = \dfrac{1}{R's} + \dfrac{1}{R''s} \\[0.5em] \dfrac{1}{Rp} = \dfrac{1}{R1 + R2} + \dfrac{1}{R3 + R4} \\[0.5em] \dfrac{1}{Rp} = \dfrac{R3 + R4 + R1 + R2}{(R1 + R2)(R3 + R4)} \\[0.5em] Rp = \dfrac{(R1 + R2)(R3 + R4)}{R1 + R2 + R3 + R4} \\[0.5em]

Hence, equivalent resistance = $\dfrac{(R$1 + R2)(R3 + R4)}{R1 + R2 + R3 + R4}