Physics
Deduce an expression for the pressure at a depth inside a liquid.
Fluids Pressure
Answer
Consider a vessel containing a liquid with density ρ. Let the liquid be stationary. In order to calculate pressure at a depth h, consider a horizontal circular surface PQ with area A at depth h below the free surface XY of the liquid as shown below.
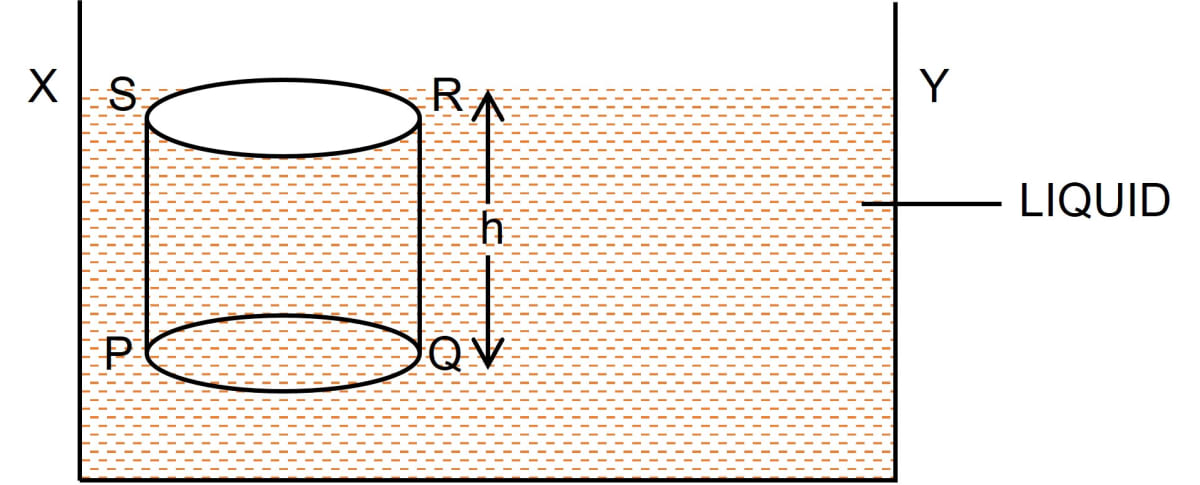
The pressure on surface PQ will be due to the weight of the liquid column above the surface PQ, (i.e., the liquid contained in cylinder PQRS of height h with PQ as it's base and top face RS lying on the free surface XY of the liquid).
Thrust exerted on the surface PQ
= Weight of the liquid column PQRS
= Volume of liquid column PQRS x density x g
= (Area of base PQ x height) x density x g
= (A x h) ρ x g = A h ρ g
This thrust is exerted on the surface PQ of area A. Therefore, pressure
P = = = h ρ g
Hence, Pressure = depth x density of liquid x acceleration due to gravity = h ρ g
Answered By
Related Questions
Name and state the principle on which a hydraulic press works. Write one use of the hydraulic press.
Describe a simple experiment to demonstrate that a liquid enclosed in a vessel exerts pressure in all directions.
Explain the principle of a hydraulic machine. Name two devices which work on this principle.
The diagram in figure shows a device which makes use of the principle of transmission of pressure.
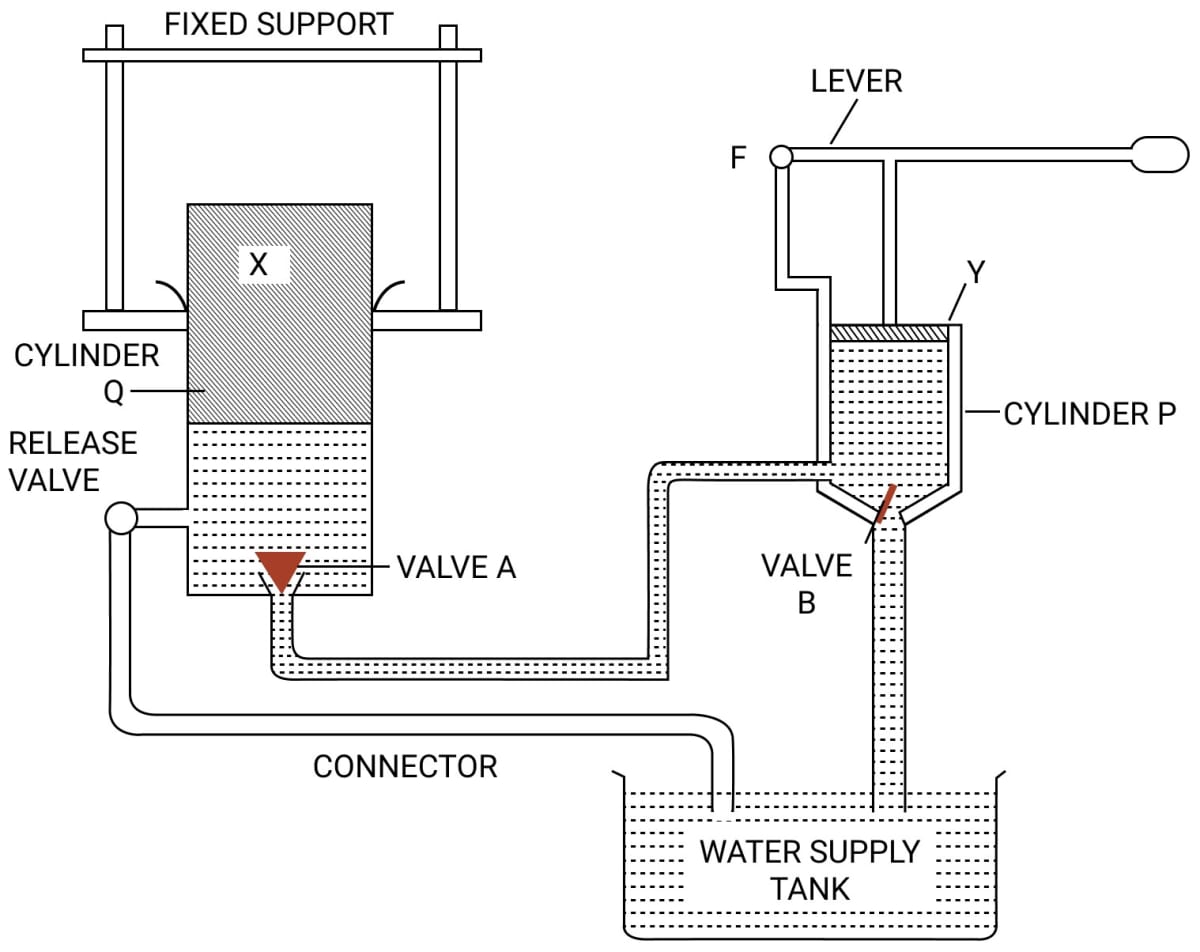
(i) Name the parts labelled by the letters X and Y.
(ii) Describe what happens to the valves A and B and to the quantity of water in the two cylinders when the lever arm is moved down.
(iii) Give reasons for what happens to the valves A and B in part (ii).
(iv) What happens when the release valve is opened ?
(v) What happens to the valve B in cylinder P when the lever arm is moved up ?
(vi) Give a reason for your answer in part (v)
(vii) State one use of the above device.