Construct a triangle ABC with the following data :

AB = 5 cm, BC = 6 cm and ∠ABC = 90°.

(i) Find a point P which is equidistant from B and C and is 5 cm from A. How many such points are there ?

(ii) Construct the inscribed circle of △ABC drawn above.

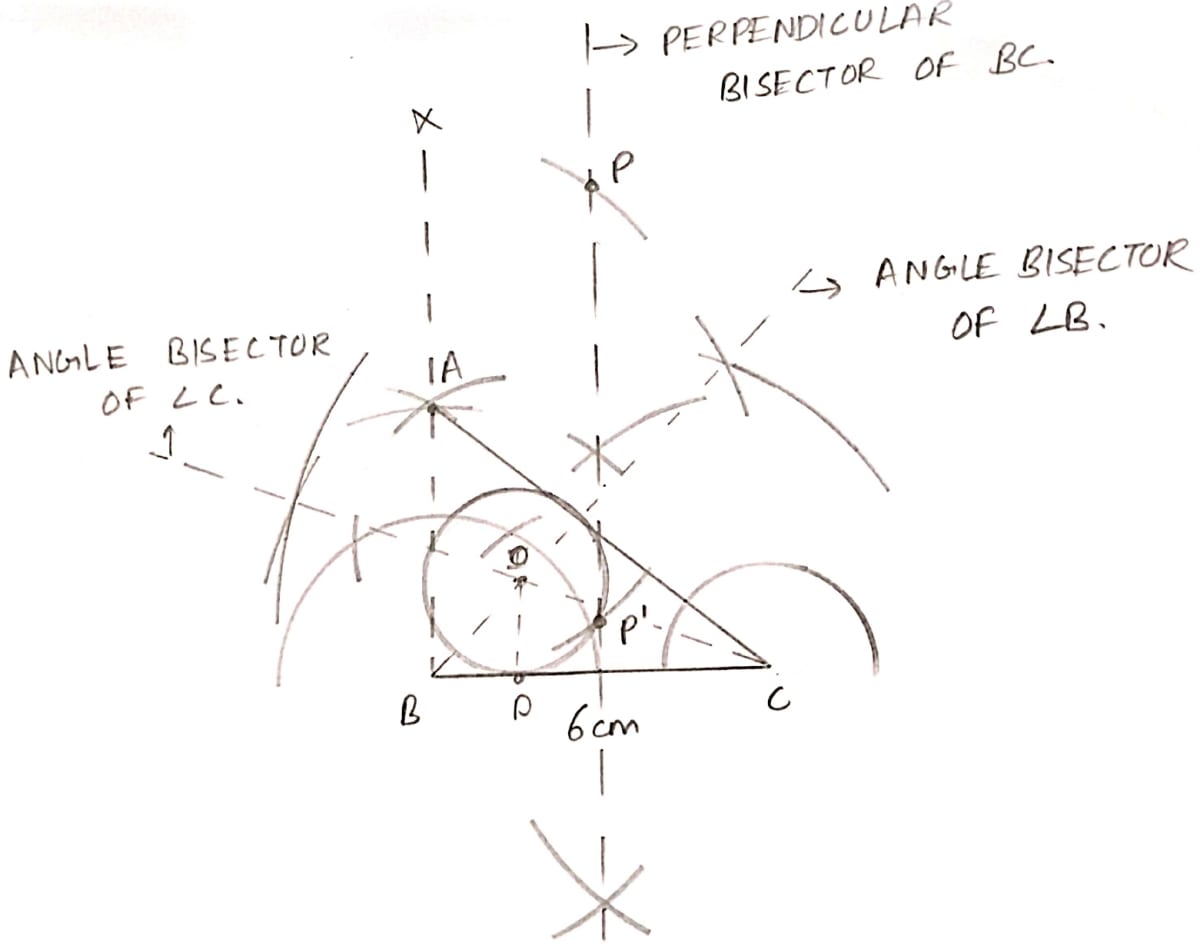
(i) Steps of construction :

1. Draw a line segment BC = 6 cm.

2. At B, draw a ray BX making an angle of 90° and cut off BA = 5 cm.

3. Join AC.

4. Draw the perpendicular bisector of BC.

5. From A with 5 cm radius, draw arc which intersects the perpendicular bisector of BC at P and P'.

There are two points (P and P') equidistant from B and C and at a distance of 5 cm from A.

(ii) Steps of construction :

1. Draw the angle bisectors of ∠B and ∠C intersecting at O.

2. From O, draw OD ⊥ BC.

3. With centre O and radius OD, draw a circle which will touch the sides AB and BC.

Hence, the required inscribed circle of △ABC is formed.