Mathematics
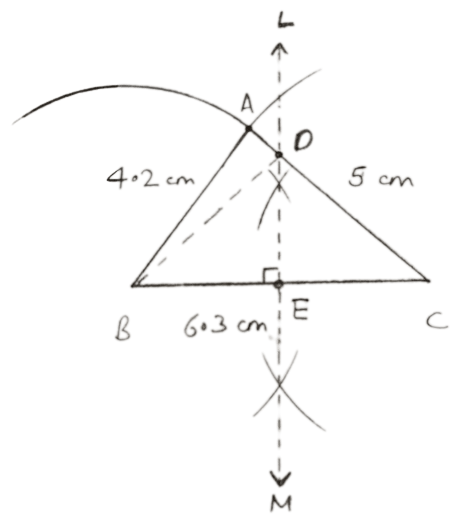
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
Answer
Steps of Construction:
Draw a line segment BC = 6.3 cm
With centre B and radius 4.2 cm, draw an arc.
With centre C and radius 5 cm, draw another arc which intersects the first arc at A.
Join AB and AC. Then, ∆ABC is the required triangle.
Draw LM, perpendicular bisector of BC.
Let LM intersect AC at D and BC at E.
Join DB.
In ∆DBE and ∆DCE,
⇒ BE = EC [LM is the perpendicular bisector of BC]
⇒ ∠DEB = ∠DEC [Each 90°]
⇒ DE = DE [Common]
∴ ∆DBE ≅ ∆DCE [By SAS]
∴ DB = DC [By C.P.C.T.]
Hence, proved that D is equidistant from B and C.
Related Questions
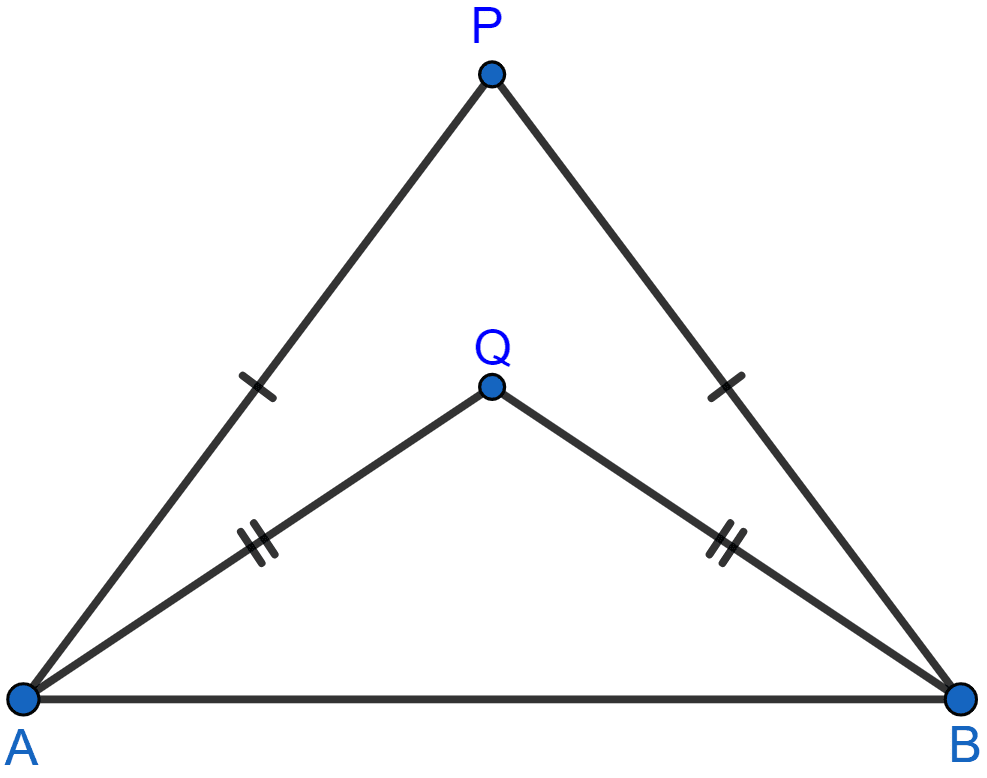
In each of the given figures; PA = PB and QA = QB.
(i)
(ii)
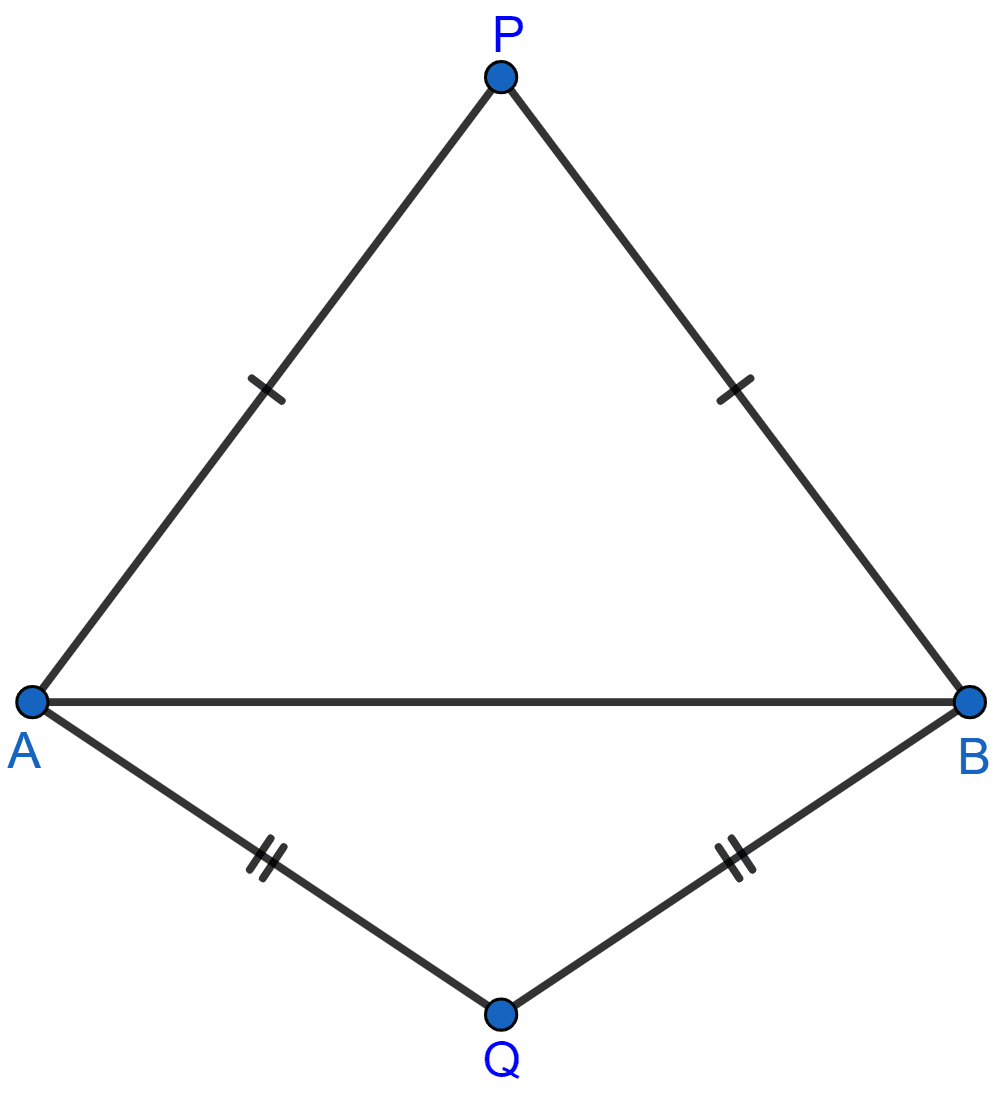
Prove in each case, that PQ (produce, if required) is perpendicular bisector of AB.
Hence, state the locus of the points equidistant from two given fixed points.
Construct a triangle ABC in which angle ABC = 75°, AB = 5 cm and BC = 6.4 cm. Draw perpendicular bisector of side BC and also the bisector of angle ACB. If these bisectors intersect each other at point P; prove that P is equidistant from B and C; and also from AC and BC.
Given: CP is the bisector of angle C of ∆ABC.
Prove: P is equidistant from AC and BC.

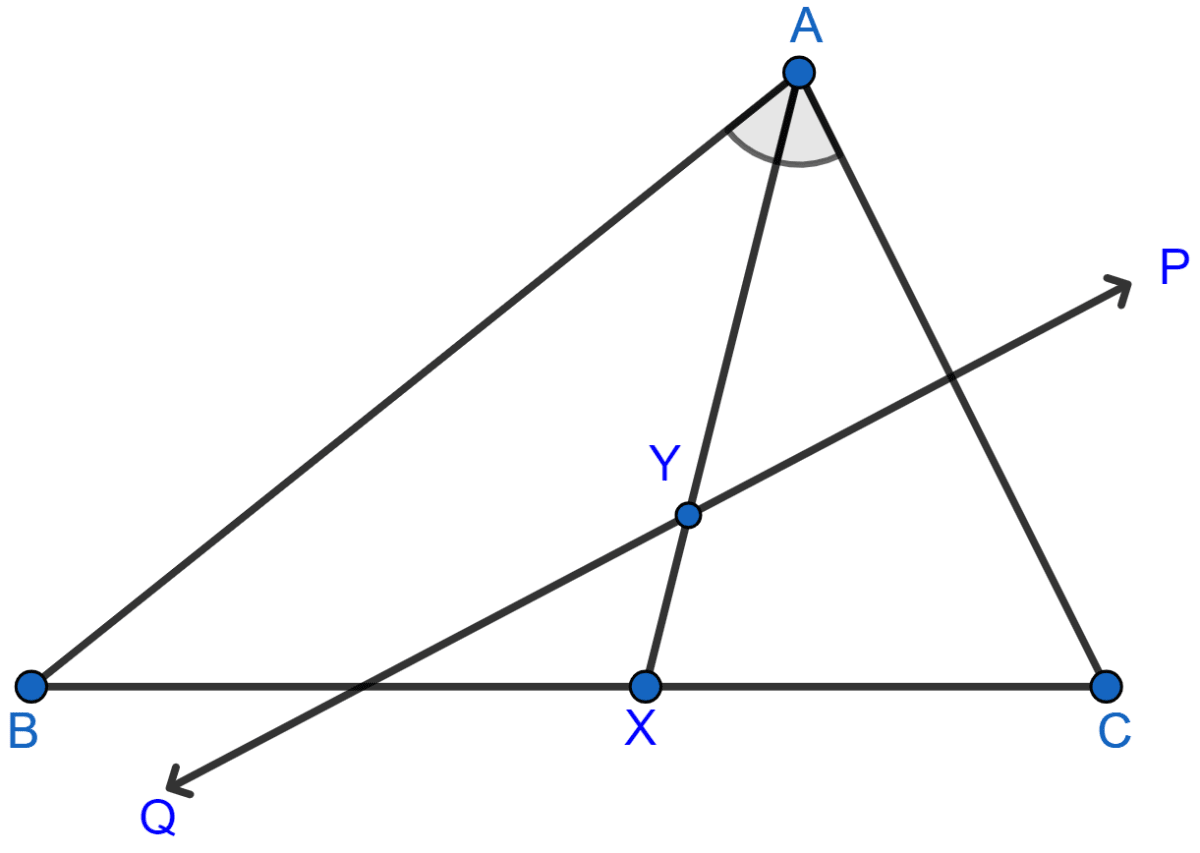
Given: AX bisects angle BAC and PQ is perpendicular bisector of AC which meets AX at point Y.
Prove :
(i) X is equidistant from AB and AC.
(ii) Y is equidistant from A and C.