Mathematics
Construct a right angled triangle PQR, in which ∠Q = 90°, hypotenuse PR = 8 cm and QR = 4.5 cm. Draw bisector of angle PQR and let it meet PR at point T. Prove that T is equidistant from PQ and QR.
Answer
Steps of Construction:
Draw a line segment QR = 4.5 cm
At Q, draw a ray QX making an angle of 90°.
With centre R and radius 8 cm, draw an arc which intersects QX at P.
Join RP. ∆PQR is the required triangle.
Draw the bisector of ∠PQR which meets PR at T.
From T, draw perpendicular TL and TM on PQ and QR, respectively.
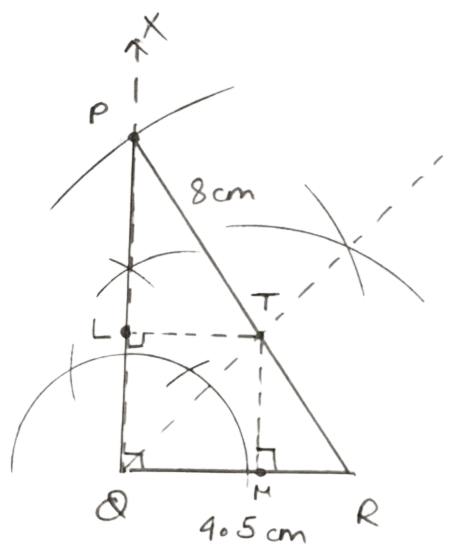
In ∆LTQ and ∆MTQ
∠TLQ = ∠TMQ [Each 90°]
∠LQT = ∠TQM [QT is angle bisector]
QT = QT [Common]
∴ ∆LTQ ≅ ∆MTQ [By AAS axiom]
∴ TL = TM [By C.P.C.T.]
Hence, proved that T is equidistant from PQ and QR.