Mathematics
Construct a regular hexagon ABCDEF of side 4.3 cm and construct its circumscribed circle. Also, construct tangents to the circumscribed circle at points B and C which meets each other at point P. Measure and record ∠BPC.
(Use a ruler and a compass for this question.)
Constructions
29 Likes
Answer
We know that each angle in a regular hexagon = 120°.
Draw a line segment AB = 4.3 cm.
At A and B draw rays making an angle of 120° each and cut off AF = BC = 4.3 cm.
At F and C, draw rays making angle of 120° each and cut off EF = CD = 4.3 cm.
Join ED. Hence, ABCDEF is the required hexagon.
Draw the perpendicular bisector of AB and AF. Let these bisectors meet at the point O.
With O as center and radius equal to OA or OB draw a circle which passes through the vertices of the hexagon. This is the required circumcircle of hexagon ABCDEF.
Draw the radius OB and OC.
At point B, construct a line perpendicular to OB. This line is the tangent at B.
At point C, construct a line perpendicular to OC. This line is the tangent at C.
The two tangents will intersect at point P.
Measure ∠BPC.
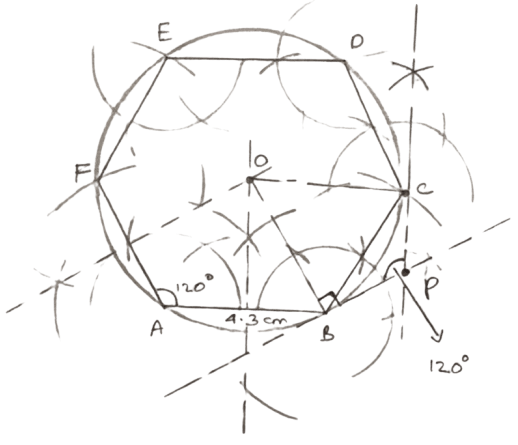
Hence, ∠BPC = 120°.
Answered By
19 Likes
Related Questions
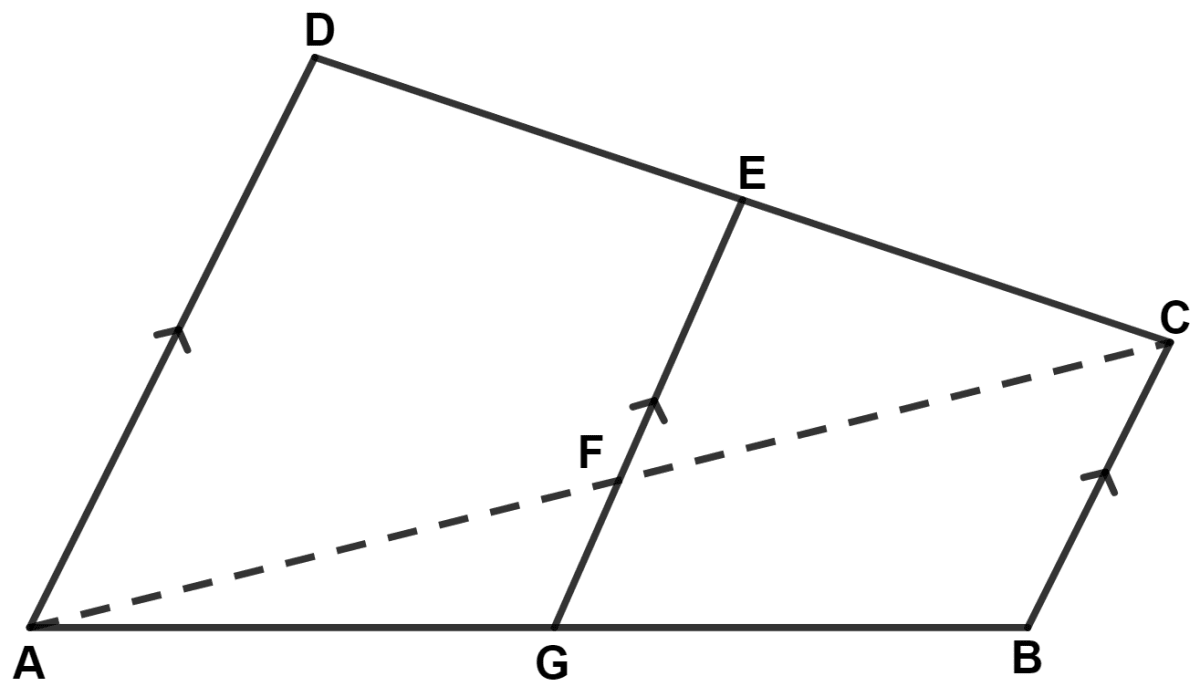
In the figure given below (not drawn to scale), AD ∥ GE ∥ BC, DE = 18 cm, EC = 3 cm, AD = 35 cm. Find :
(a) AF : FC
(b) length of EF
(c) area(trapezium ADEF) : area(Δ EFC)
(d) BC ∶ GF
(a) Construct the locus of a moving point which moves such that it keeps a fixed distance of 4.5 cm from a fixed-point O.
(b) Draw line segment AB of 6 cm where A and B are two points on the locus (a).
(c) Construct the locus of all points equidistant from A and B. Name the points of intersection of the loci (a) and (c) as P and Q respectively.
(d) Join PA. Find the locus of all points equidistant from AP and AB.
(e) Mark the point of intersection of the locus (a) and (d) as R. Measure and write down the length of AR.
(Use a ruler and a compass for this question.)
A mathematics teacher uses certain amount of terracotta clay to form different shaped solids. First, she turned it into a sphere of radius 7 cm and then she made a right circular cone with base radius 14 cm. Find the height of the cone so formed. If the same clay is turned to make a right circular cylinder of height cm, then find the radius of the cylinder so formed. Also, compare the total surface areas of sphere and cylinder so formed.
A tree (TS) of height 30 m stands in front of a tall building (AB). Two friends Rohit and Neha are standing at R and N respectively, along the same straight line joining the tree and the building (as shown in the diagram). Rohit, standing at a distance of 150 m from the foot of the building, observes the angle of elevation of the top of the building as 30°. Neha from her position observes that the top of the building and the tree has the same elevation of 60°.
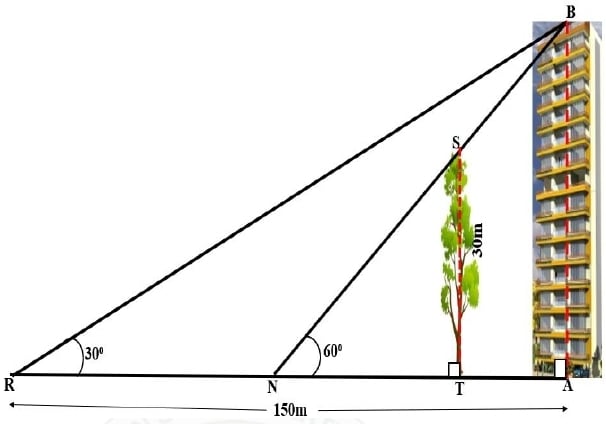
Find the:
(a) height of the building
(b) distance between
- Neha and the foot of the building
- Rohit and Neha
- Neha and the tree
- building and the tree.