Mathematics
Calculate the other sides of a triangle whose shortest side is 6cm and which is similar to a triangle whose sides are 4cm, 7cm and 8cm.
Similarity
42 Likes
Answer
Let △ABC ~ △DEF in which shortest side of △ABC be BC = 6cm.
△DEF, DE = 8cm, EF = 4cm and DF = 7cm.
Since, △ABC ~ △DEF so,
Now consider,
Hence, the other sides of triangle are 10.5cm and 12cm.
Answered By
24 Likes
Related Questions
If △ABC ~ △DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, then find the perimeter of △ABC.
If △ABC ~ △PQR, perimeter of △ABC = 32cm, perimeter of △PQR = 48cm and PR = 6cm, then find the length of AC.
In the figure given below, AB ∥ DE, AC = 3cm, CE = 7.5cm and BD = 14cm. Calculate CB and DC.
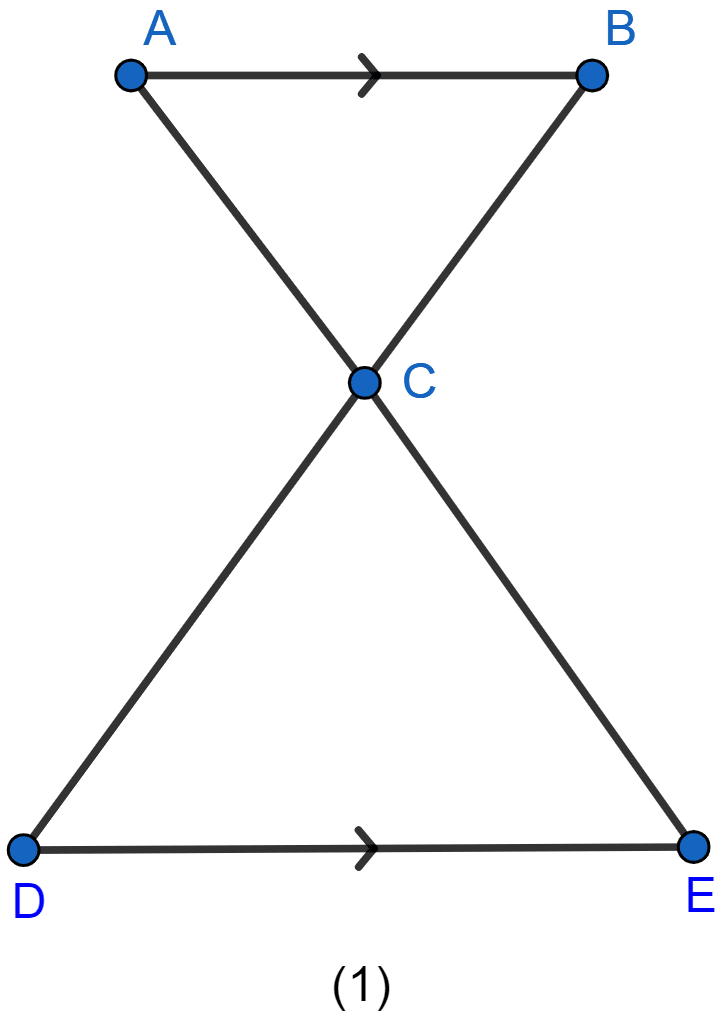
In the figure (2) given below, CA ∥ BD, the lines AB and CD meet at O.
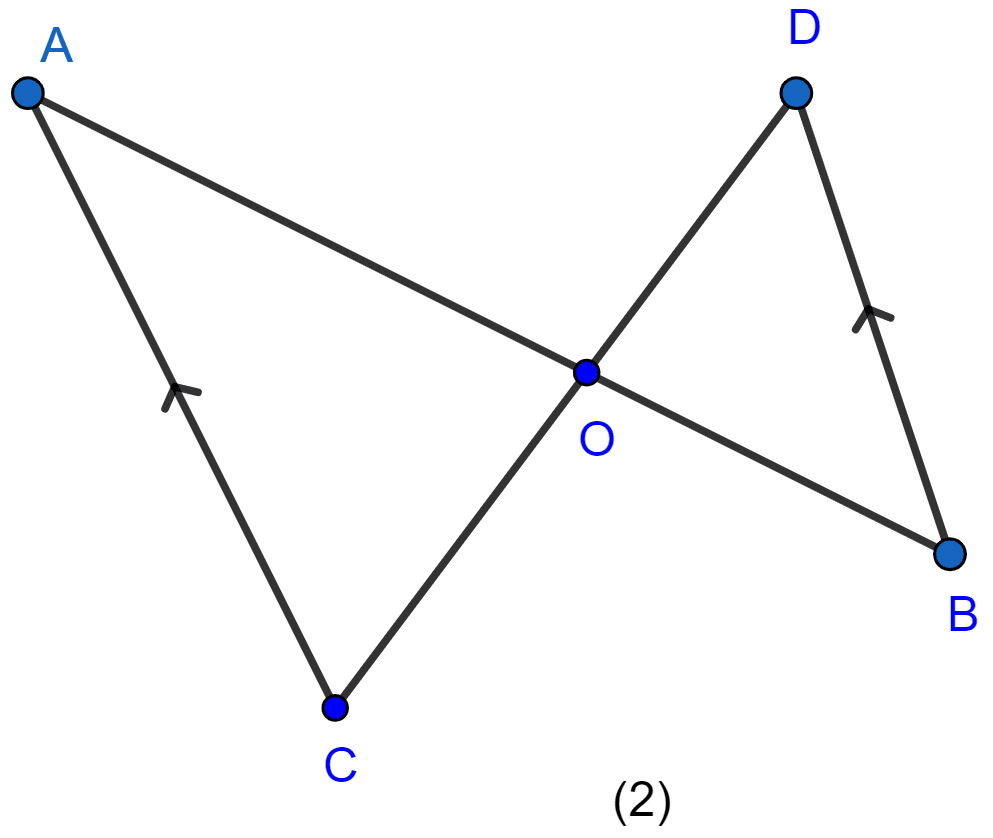
(i) Prove that △ACO ~ △BDO.
(ii) If BD = 2.4 cm, OD = 4 cm, OB = 3.2 cm and AC = 3.6 cm, calculate OA and OC.