Mathematics
A and B are two points on the x-axis and y-axis respectively.
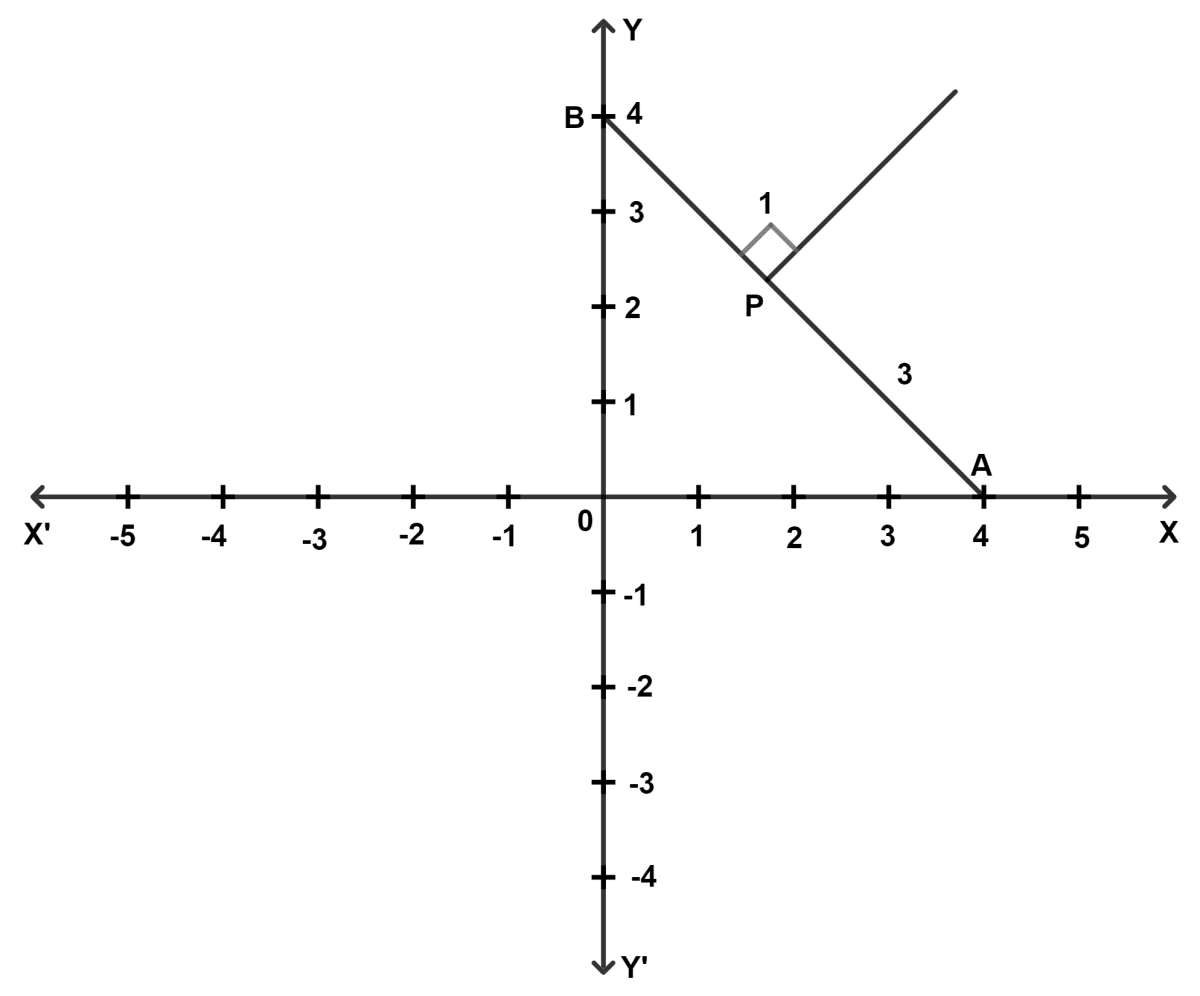
(a) Write down the co-ordinates of A and B.
(b) P is a point on AB such that AP : PB = 3 : 1. Using section formula find the coordinates of point P.
(c) Find the equation of a line passing through P and perpendicular to AB.
Section Formula
ICSE 2023
8 Likes
Answer
(a) From figure,
A = (4, 0) and B = (0, 4).
(b) Let coordinates of P be (x, y).
By section formula,
(x, y) = 1x2 + m2x1}{m1 + m2}, \dfrac{m1y2 + m2y1}{m1 + m2}\Big)
Substituting values we get :
Hence, coordinates of P = (1, 3).
(c) By formula,
Slope = 2 - y1}{x2 - x1}
Substituting values we get :
Slope of AB = = -1.
We know that,
Product of slope of perpendicular lines = -1.
∴ Slope of AB × Slope of line perpendicular to AB = -1
⇒ -1 × Slope of line perpendicular to AB = -1
⇒ Slope of line perpendicular to AB = = 1.
Line passing through P and perpendicular to AB :
⇒ y - y1 = m(x - x1)
⇒ y - 3 = 1(x - 1)
⇒ y - 3 = x - 1
⇒ y = x - 1 + 3
⇒ y = x + 2.
Hence, required equation is y = x + 2.
Answered By
4 Likes
Related Questions
The following distribution gives the daily wages of 60 workers of a factory.
Daily income in ₹ Number of workers 200-300 6 300-400 10 400-500 14 500-600 16 600-700 10 700-800 4 Use graph paper to answer this question.
Take 2 cm = ₹ 100 along one axis and 2 cm = 2 workers along the other axis. Draw a histogram and hence find the mode of the give distribution.
The 5th and 9th term of an Arithmetic Progression are 4 and -12 respectively. Find :
(a) the first term
(b) common difference
(c) sum of 16 terms of the A.P.
A bag contains 25 cards, numbered through 1 to 25. A card is drawn at random. What is the probability that the number on the card drawn is :
(a) a multiple of 5
(b) a perfect square
(c) a prime number ?
A man covers a distance of 100 km, travelling with a uniform speed of x km/hr. Had the speed been 5 km/hr more it would have taken 1 hour less. Find x the original speed.