Mathematics
Arcs AB and BC are of lengths in the ratio 11 : 4 and O is center of the circle. If angle BOC = 32°, the angle AOB is :
64°
88°
128°
132°

Circles
7 Likes
Answer
Given,
Arcs AB and BC are of lengths in the ratio 11 : 4.
∴ ∠AOB : ∠BOC = 11 : 4
⇒ ∠AOB : 32° = 11 : 4
⇒ ∠AOB = = 88°.
Hence, Option 2 is the correct option.
Answered By
2 Likes
Related Questions
In the given figure x°, y°, z° and p° are exterior angles of cyclic quadrilateral ABCD, then x° + y° + z° + p° is :
180°
270°
360°
720°

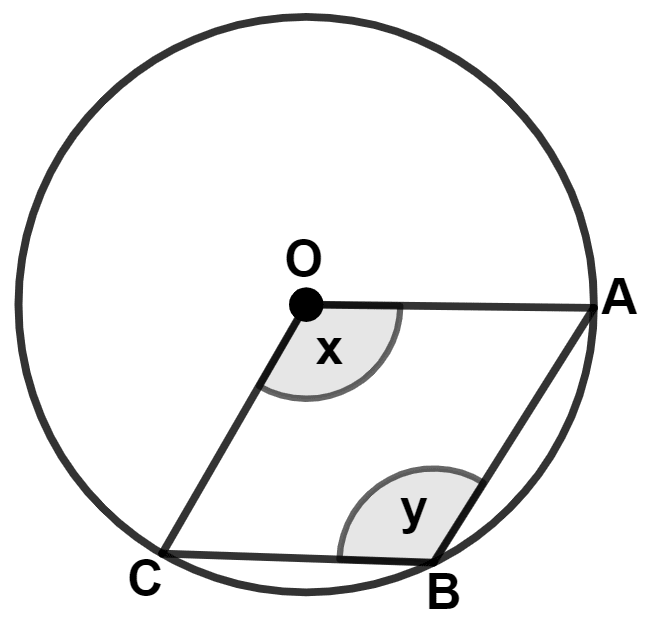
In the given figure, O is center of the circle and OABC is a rhombus, then :
x° + y° = 180°
x° = y° = 90°
x° + 2y° = 360°
x° = y° = 45°
In the given figure, AB is the side of regular pentagon and BC is the side of regular hexagon. Angle BAC is :
132°
66°
90°
120°
In the given figure, O is center of the circle. Chord BC = chord CD and angle A = 80°. Angle BOC is :
120°
80°
100°
160°
