Mathematics
An aircraft is flying at a constant height with a speed of 360 km/h. From a point on the ground, the angle of elevation of the aircraft at an instant was observed to be 45°. After 20 seconds, the angle of elevation was observed to be 30°. Determine the height at which the aircraft is flying (use = 1.732).
Heights & Distances
115 Likes
Answer
Speed of aircraft = 360 km/h
Distance covered in 20 seconds = km
Let aeroplane be flying at a hight of h km.
E is the fixed point on ground and A is the initial position of aircraft and C is the position after 20 seconds.
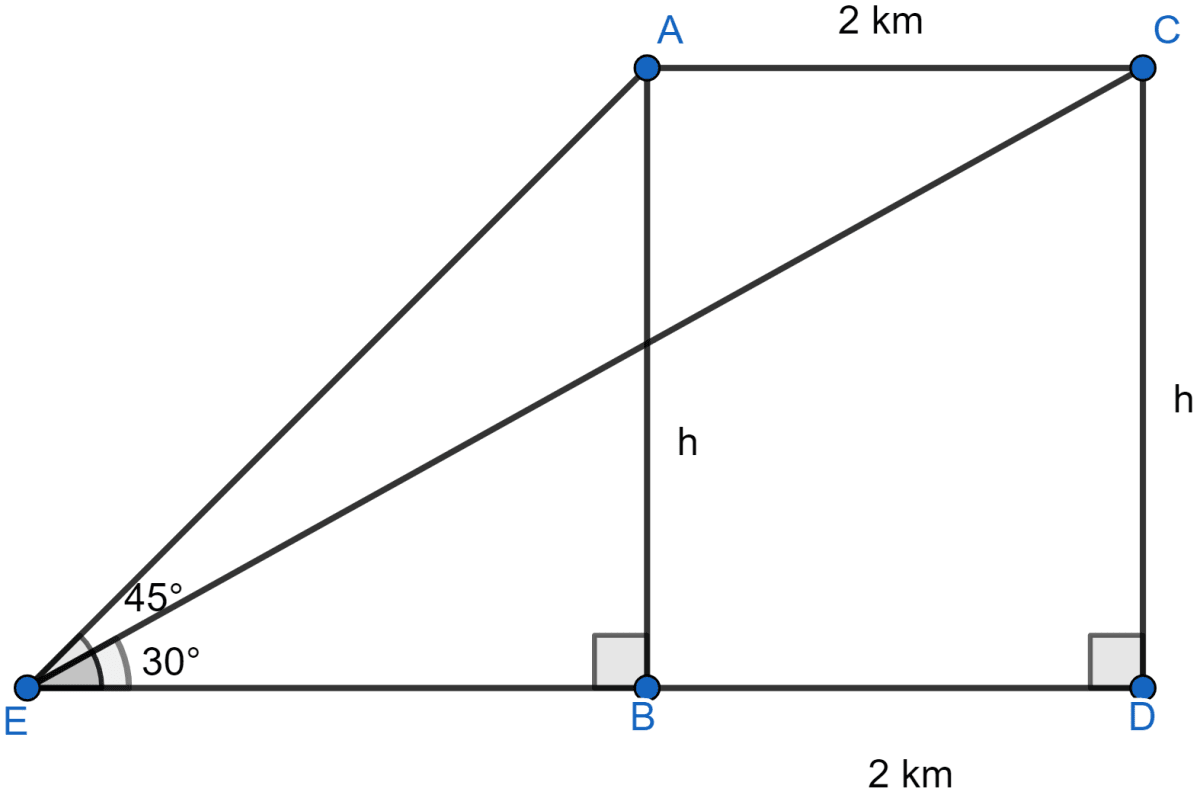
Considering right angled △EDC we get,
From figure,
Considering right angled △AEB we get,
Comparing Eq 1 and Eq 2 we get,
Hence, the aircraft is flying at a height of 2732 meters.
Answered By
31 Likes
Related Questions
From the top of a building 20 m high, the angle of elevation of the top of a monument is 45° and the angle of depression of its foot is 15°. Find the height of the monument.
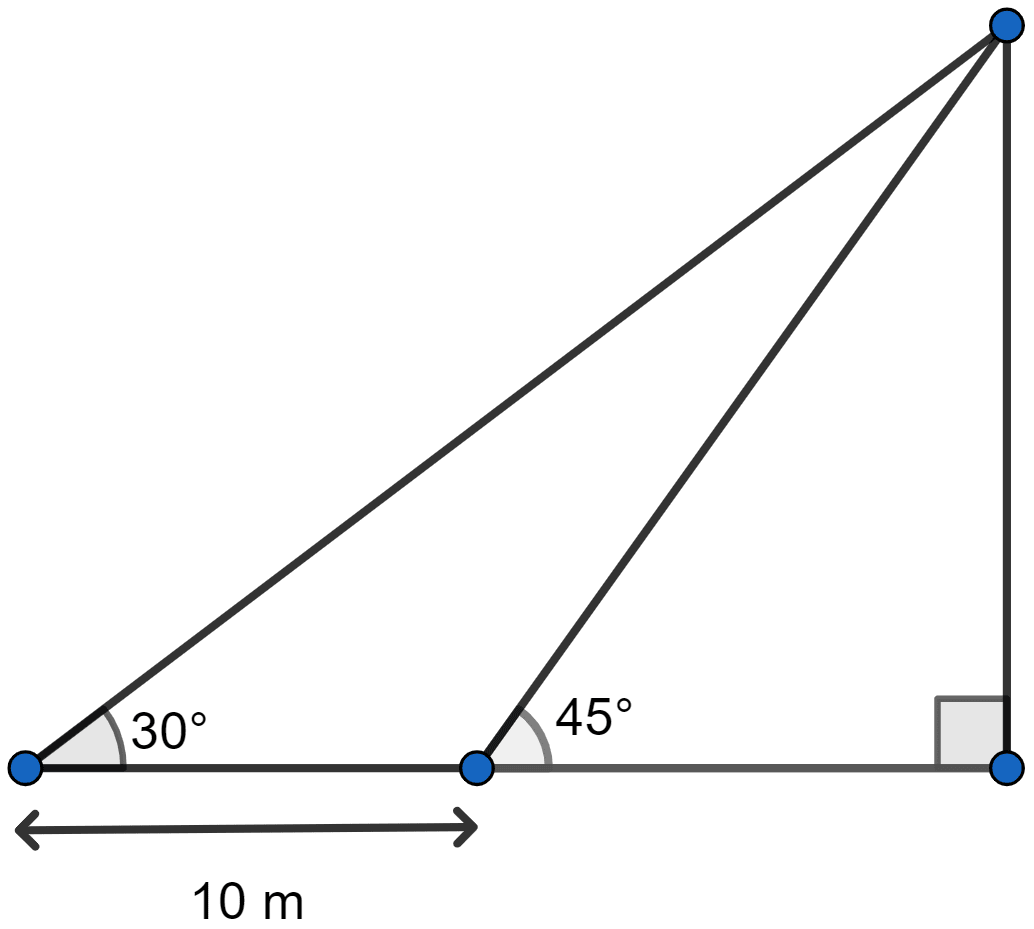
In the adjoining figure, the shadow of a vertical tower on the level ground increases by 10 m, when the altitude of the sun changes from 45° to 30°. Find the height of the tower and give your answer, correct to of a metre.
If a kite is flying at a height of meters from the level ground, attached to a string inclined at 60° to the horizontal, then the length of the string is
80 m
m
m
120 m.
If the angle of depression of an object from a 75 m high tower is 30°, then the distance of the object from the tower is
m
m
m
150 m