Mathematics
ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ; prove that AP and DQ are perpendicular to each other.
Answer
Let AP and DQ intersect at point O.
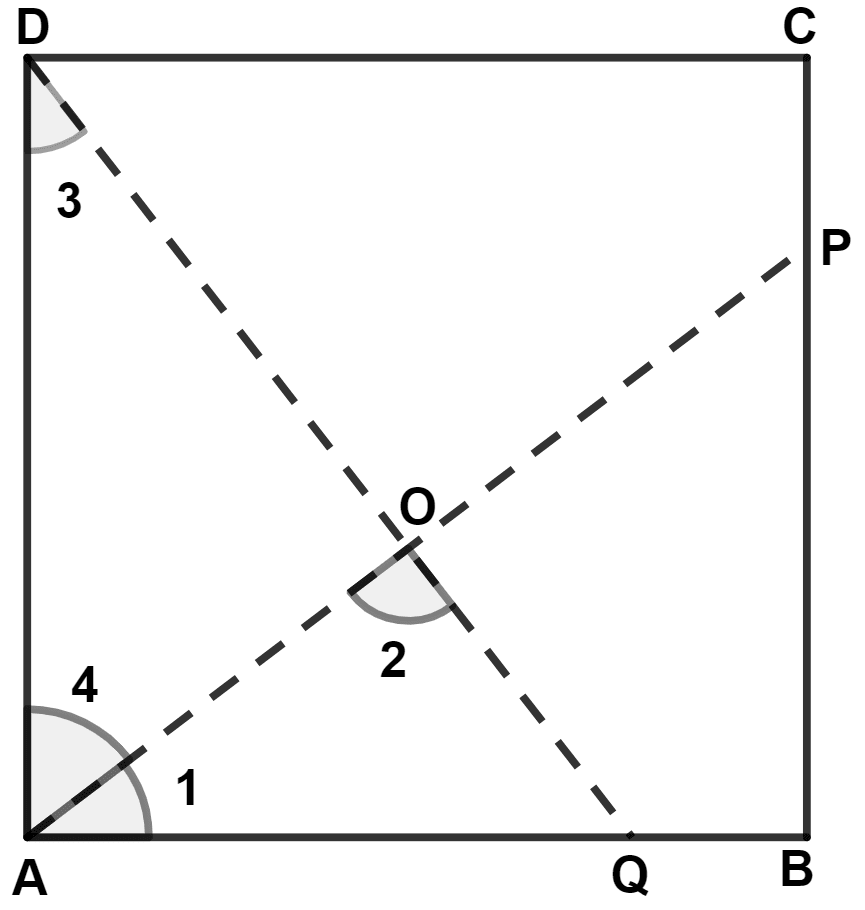
In △ DAQ and △ ABP,
⇒ ∠DAQ = ∠ABP (Interior angle of square equal to 90°)
⇒ DQ = AP (Given)
⇒ AD = AB (Each side of square equal in length)
∴ △ DAQ ≅ △ ABP (By R.H.S. congruence rule)
We know that,
Corresponding parts of congruent triangle are equal.
∴ ∠3 = ∠1 ……..(1)
From figure,
⇒ ∠1 + ∠4 = 90°
Substituting value of ∠1 from equation (1) in above equation, we get :
⇒ ∠3 + ∠4 = 90°
In triangle AOD,
By angle sum property of triangle,
⇒ ∠ODA + ∠OAD + ∠AOD = 180°
⇒ ∠3 + ∠4 + ∠AOD = 180°
⇒ 90° + ∠AOD = 180°
⇒ ∠AOD = 180° - 90° = 90°.
∴ AP ⊥ DQ.
Hence, proved that AP and DQ are perpendicular to each other.
Related Questions
Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.
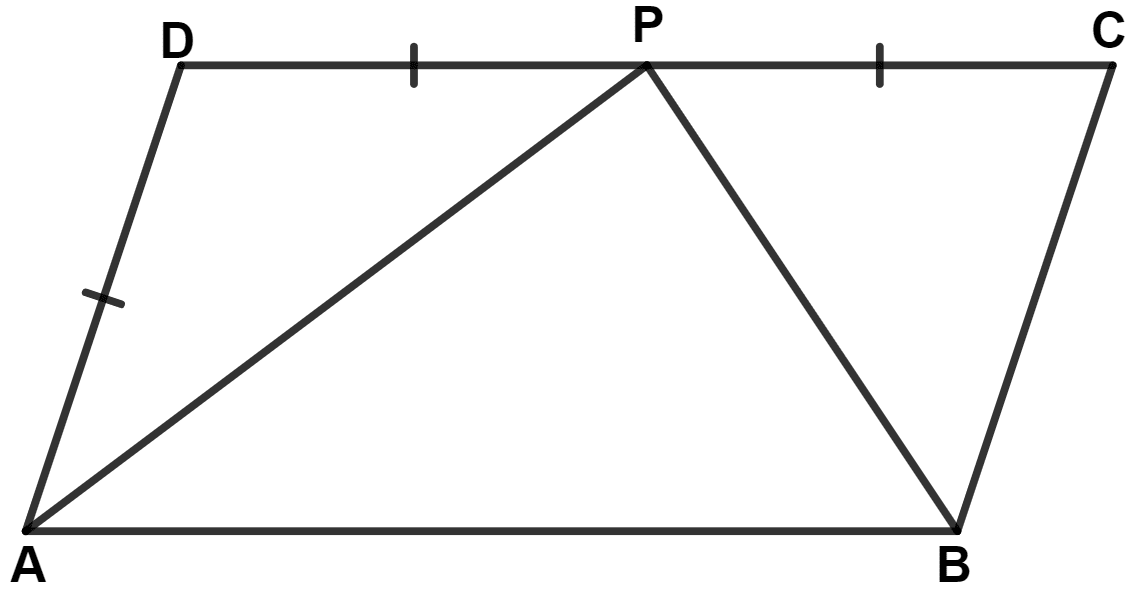
In the following figure, ABCD is a parallelogram. Prove that :
(i) AP bisects angle A
(ii) BP bisects angle B
(iii) ∠DAP + ∠CBP = ∠APB
In a quadrilateral ABCD, AB = AD and CB = CD. Prove that :
(i) AC bisects angle BAD.
(ii) AC is perpendicular bisector of BD.
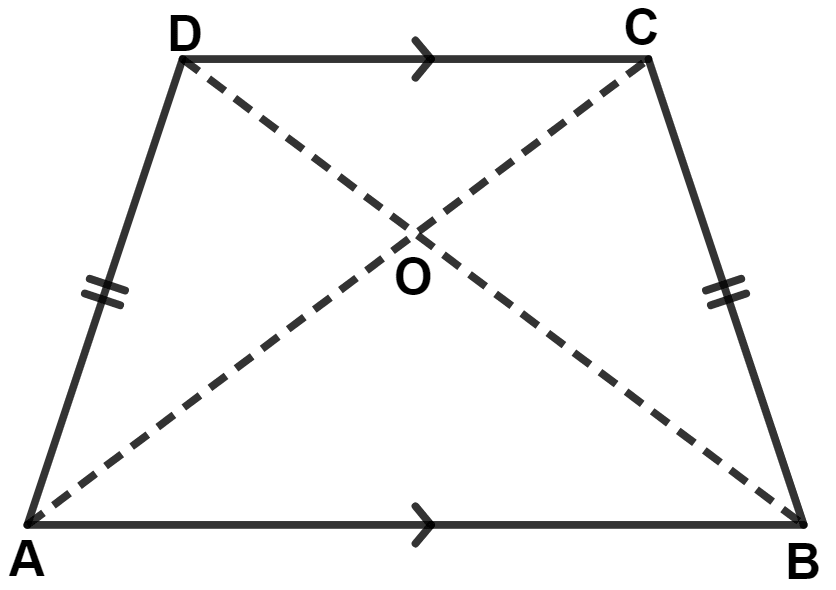
The following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC.
Prove that :
(i) ∠DAB = ∠CBA
(ii) ∠ADC = ∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD