Mathematics
AB is a diameter of a circle with centre O. Chord CD is equal to radius OC. AC and BD produced intersect at P. Prove that : ∠APB = 60°.

Circles
20 Likes
Answer

From figure,
∠ADB = 90° [Angle subtended by diameter is a right angle.]
In △COD,
OC = OD [Radius of same circle]
∴ OC = OD = CD.
So, △COD is an equilateral triangle.
∴ ∠COD = 60°.
We know that,
Angle subtended by chord in the center is double the angle in the circumference.
⇒ ∠COD = 2∠CAD
⇒ ∠CAD = ∠COD
⇒ ∠CAD = = 30°.
In △APD,
⇒ ∠PAD = ∠CAD = 30°.
⇒ ∠ADP + ∠ADB = 180° [Linear pair]
⇒ ∠ADP = 180° - ∠ADB = 180° - 90° = 90°.
By angle sum property.
⇒ ∠ADP + ∠APD + ∠PAD = 180°
⇒ 90° + ∠APD + 30° = 180°
⇒ ∠APD + 120° = 180°
⇒ ∠APD = 180° - 120°
⇒ ∠APD = 60°.
From figure,
⇒ ∠APB = ∠APD = 60°.
Hence, proved that ∠APB = 60°.
Answered By
10 Likes
Related Questions
In the given figure, AB and XY are diameters of a circle with center O. If ∠APX = 30°, find :
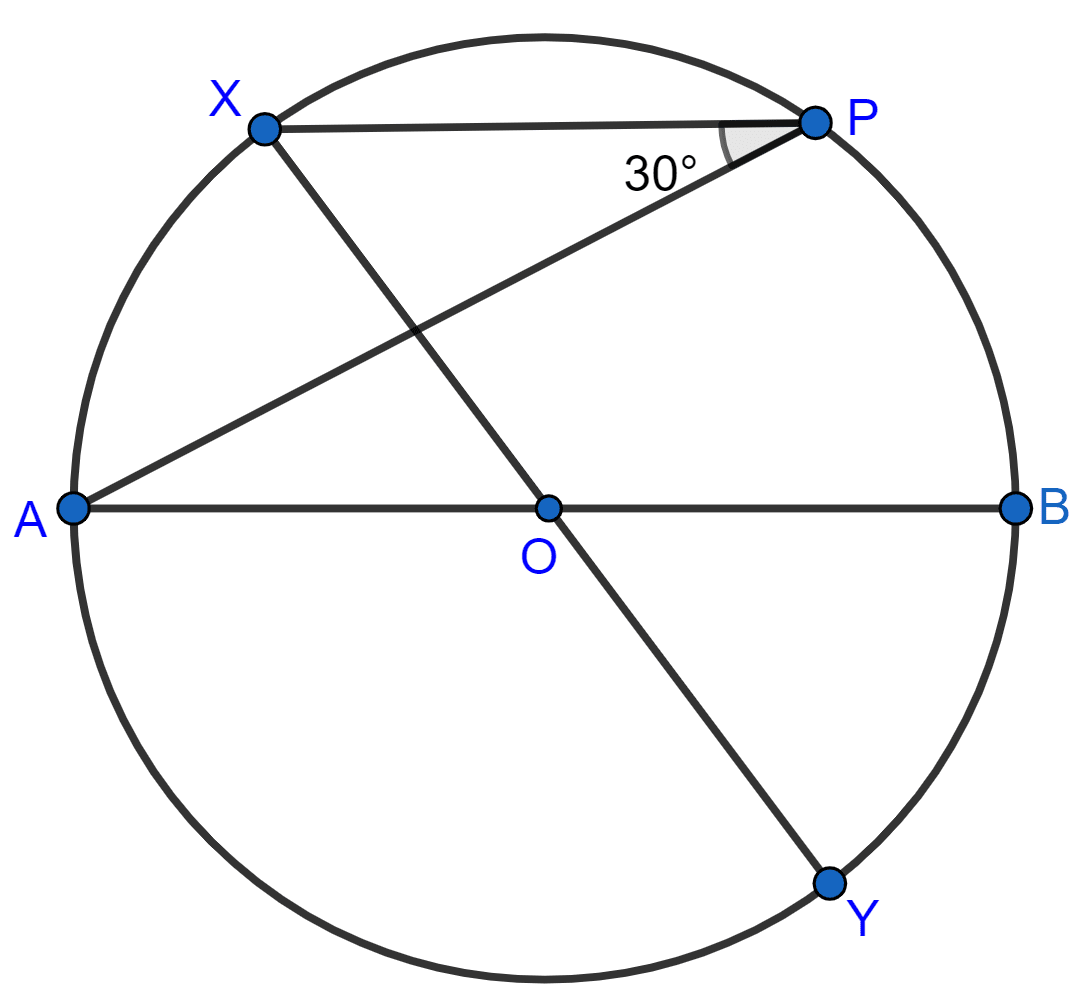
(i) ∠AOX
(ii) ∠APY
(iii) ∠BPY
(iv) ∠OAX
In the adjoining figure; AB = AD, BD = CD and ∠DBC = 2∠ABD. Prove that : ABCD is a cyclic quadrilateral.

In the given figure, AC = AB and ∠ABC = 72°. OA and OB are two tangents. Determine :
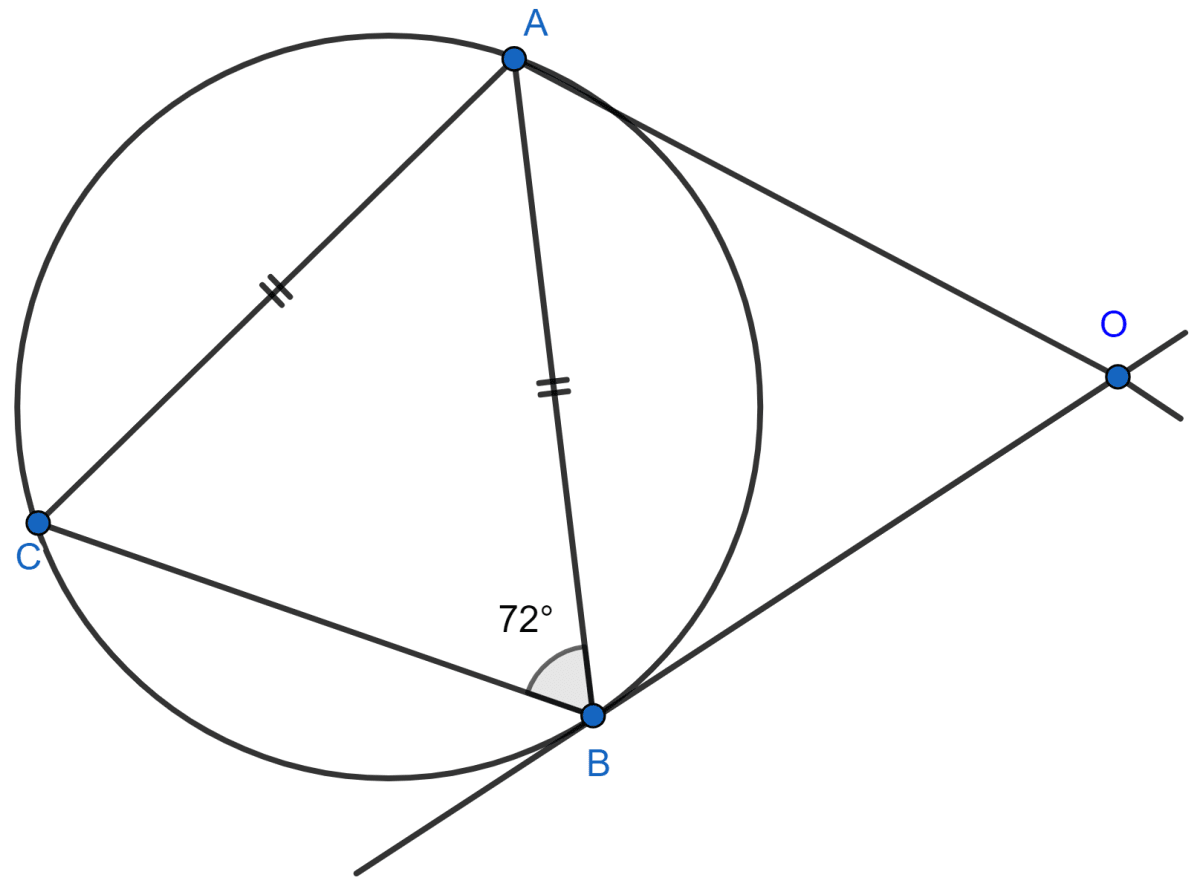
(i) ∠AOB
(ii) angle subtended by the chord AB at the center.
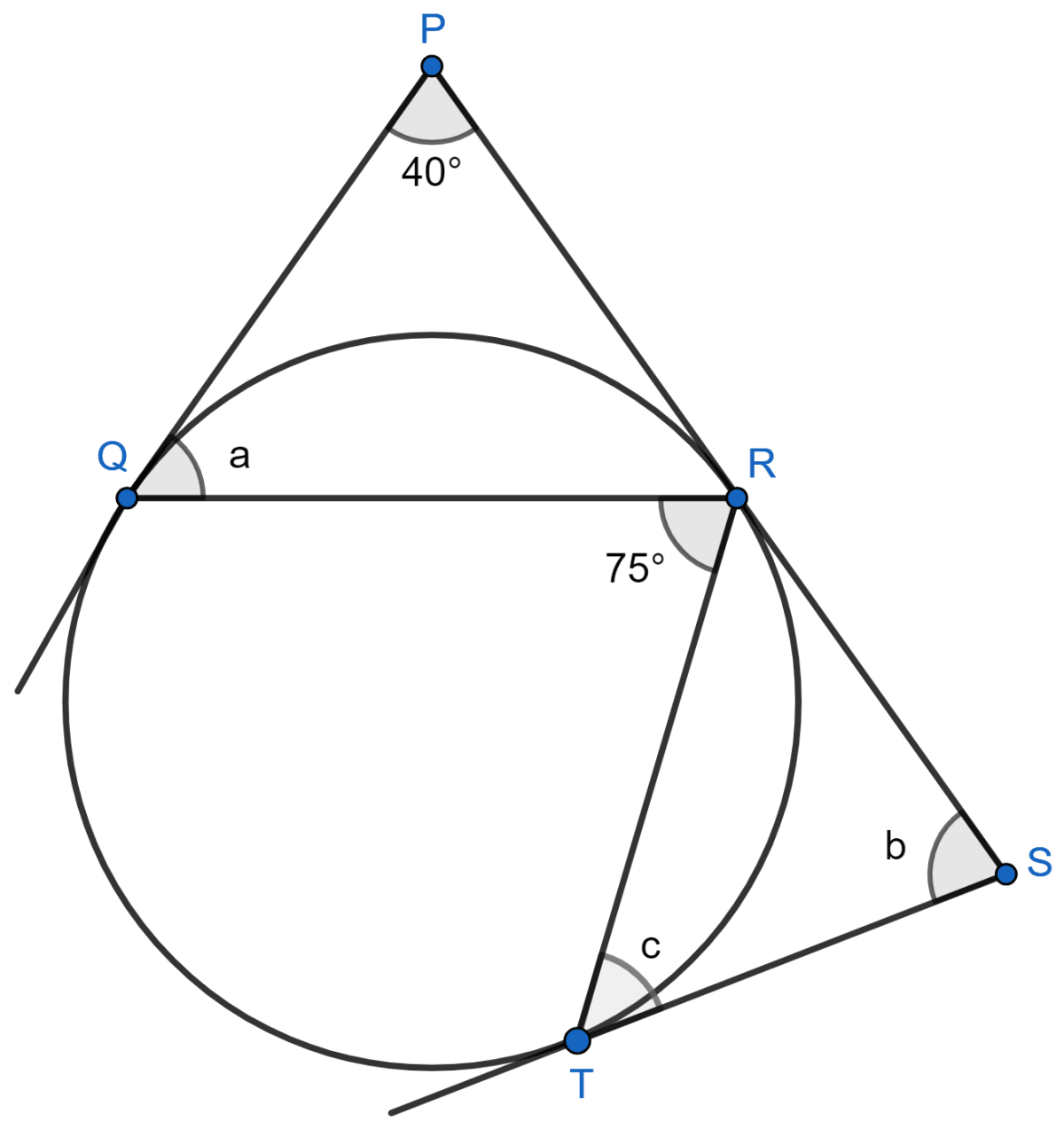
In the given figure, PQ, PR and ST are tangents to the same circle. If ∠P = 40° and ∠QRT = 75°, find a, b and c.