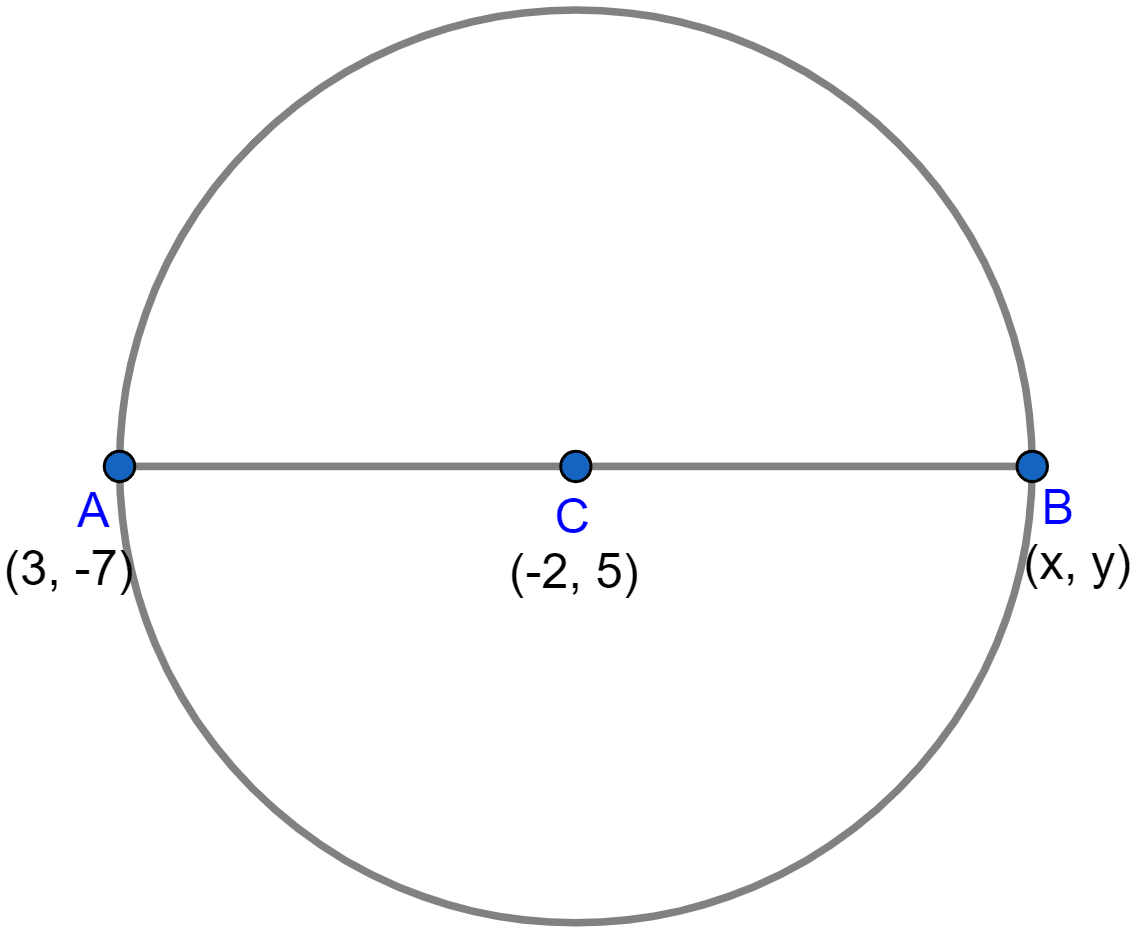
AB is a diameter of a circle with centre C(-2, 5). If the point A is (3, -7). Find :

(i) The length of radius AC.

(ii) The coordinates of B.

Below figure shows the circle with centre C(-2, 5)

(i) We know that,

Distance formula = $\sqrt{(x$2 - x1)^2 + (y2 - y1)^2}

∴ The length of radius AC = $\sqrt{(-2 - 3)^2 + (5 - (-7))^2}$

$= \sqrt{(-5)^2 + (12)^2} \\[1em] = \sqrt{25 + 144} \\[1em] = \sqrt{169} \\[1em] = 13.$

Hence, the length of radius AC is 13 units.

(ii) Given, AB is the diameter and C is the mid-point

Let coordinates of B are (x, y) so, by mid-point formula,

$\dfrac{(3 + x)}{2} = -2 \text{ and } \dfrac{(y - 7)}{2} = 5$
⇒ 3 + x = -4 and y - 7 = 10
⇒ x = -4 - 3 and y = 10 + 7
⇒ x = -7 and y = 17.

Hence, coordinates of B are (-7, 17).