A(2, -4), B(3, 3) and C(-1, 5) are the vertices of triangle ABC. Find the equation of :

(i) the median of the triangle through A.

(ii) the altitude of the triangle through B.

Triangle ABC with vertices A(2, -4), B(3, 3) and C(-1, 5) is shown below:

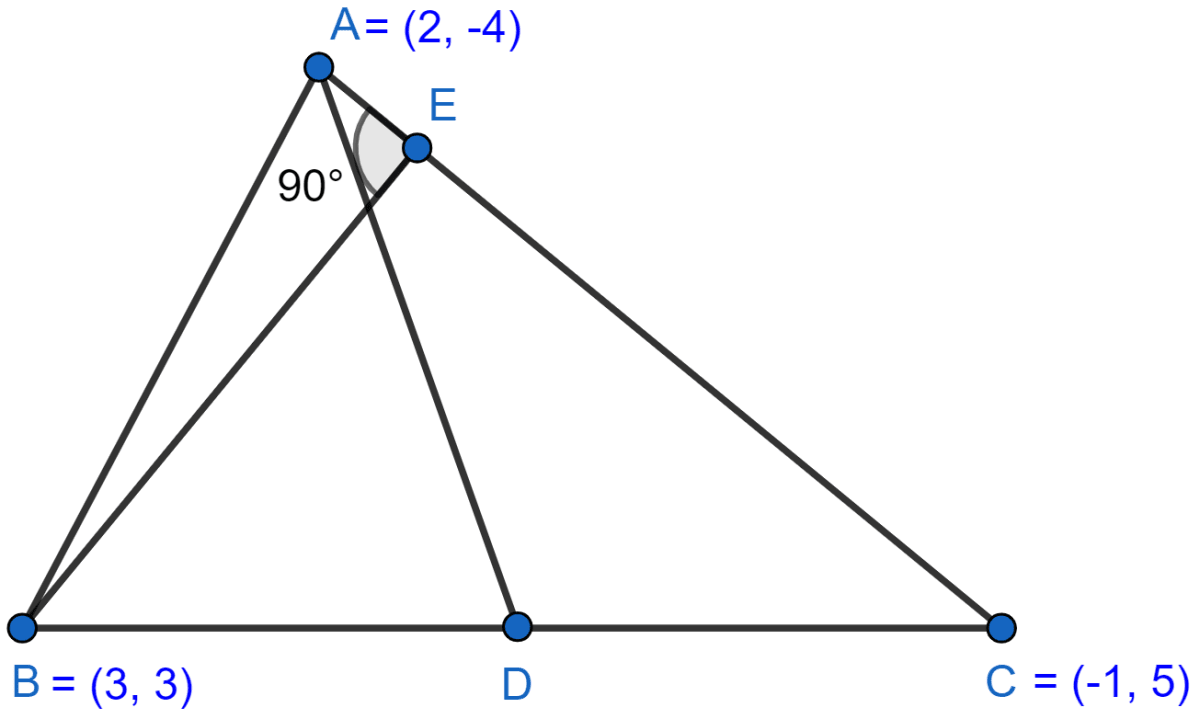
(i) Let D be the mid-point of BC. So, AD will be the median.

Coordinates of D by mid-point formula will be,

$= \Big(\dfrac{x$1 + x2}{2}, \dfrac{y1 + y2}{2}\Big) \\[1em] = \Big(\dfrac{3 + (-1)}{2}, \dfrac{3 + 5}{2}\Big) \\[1em] = \Big(\dfrac{2}{2}, \dfrac{8}{2}\Big) \\[1em] = (1, 4).

The equation of AD can be given by two-point formula i.e.,

$\Rightarrow y - y$1 = \dfrac{y2 - y1}{x2 - x1}(x - x1) \\[1em] \Rightarrow y - (-4) = \dfrac{4 - (-4)}{1 -2}(x - 2) \\[1em] \Rightarrow y + 4 = -8(x - 2) \\[1em] \Rightarrow y + 4 = -8x + 16 \\[1em] \Rightarrow 8x + y - 12 = 0.

Hence, the equation of the median of the triangle through A is 8x + y - 12 = 0.

(ii) Let E be a point on AC such that BE is perpendicular to AC.

Slope (m₁) of AC is,

$\text{m}_1 = \dfrac{5 - (-4)}{-1 - 2} \\[1em] = -\dfrac{9}{3} \\[1em] = -3.$

Let slope of BE be m₂. Since, BE is perpendicular to AC so,

$\Rightarrow m$1 \times m2 = -1 \\[1em] \Rightarrow -3 \times m2 = -1 \\[1em] \Rightarrow m2 = \dfrac{1}{3}.

So, the equation of BE by point-slope form will be

$\Rightarrow y - y$1 = m(x - x1) \\[1em] \Rightarrow y - 3 = \dfrac{1}{3}(x - 3) \\[1em] \Rightarrow 3(y - 3) = x - 3 \\[1em] \Rightarrow 3y - 9 = x - 3 \\[1em] \Rightarrow x - 3y + 6 = 0.

Hence, the equation of the required line is x - 3y + 6 = 0.