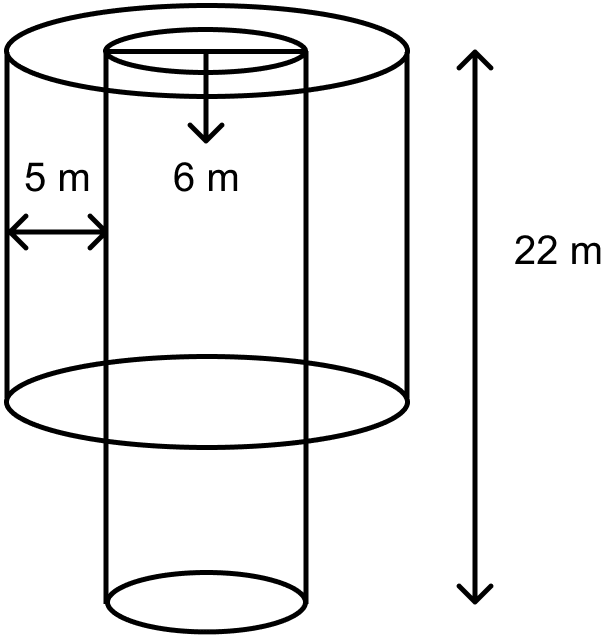
A well with inner diameter 6 m is dug 22 m deep. Soil taken out of it has been spread evenly all round it to a width of 5 m to form an embankment. Find the height of the embankment.

Inner diameter of well = 6 m

Radius of well, r = $\dfrac{6}{2}$ = 3 m.

Depth (h) = 22 m.

Volume of soil dug out of well = πr²h = π × 3² × 22 = 198π m³.

Width of embankment = 5 m.

Inner radius of embankment = Inner radius of well = r = 3 m.

Outer radius of embankment (R) = inner radius + width = 3 + 5 = 8 m.

Let H be the height of soil embankment.

Volume of soil embankment (V) = π(R² - r²)H

$V = π \times (8^2 - 3^2) \times H \\[1em] = π \times (64 - 9) \times H \\[1em] = 55πH \text{ m}^3.$

Volume of soil dug out = Volume of soil embankment.

∴ 198π = 55πH

⇒ 55H = 198 (Dividing both sides by π)

⇒ H = $\dfrac{198}{55}$ = 3.6 m

Hence, the height of the soil embankment is 3.6 m.