A vessel in the form of an inverted cone is filled with water to the brim. Its height is 20 cm and diameter is 16.8 cm. Two equal solid cones are dropped in it so that they are fully submerged. As a result, one third of the water in the original cone overflows. What is the volume of each of the solid cone submerged ?

Height of cone (h) = 20 cm.

Radius of cone (r) = $\dfrac{16.8}{2}$ = 8.4 cm.

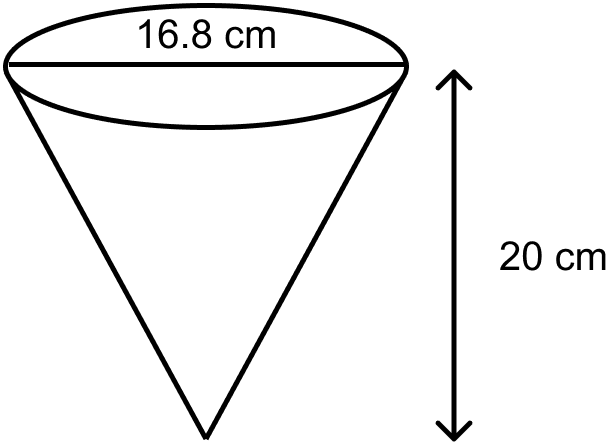
Volume of water in vessel = $\dfrac{1}{3}πr^2h$

$= \dfrac{1}{3} \times \dfrac{22}{7} \times (8.4)^2 \times 20 \\[1em] = \dfrac{22}{21} \times 70.56 \times 20 \\[1em] = \dfrac{31046.4}{21} \\[1em] = 1478.4 \text{ cm}^3.$

Given,

Volume of water overflown = One-third of the volume of water in the vessel = $\dfrac{1}{3} \times 1478.4 = 492.8$ cm³.

Volume of water overflown = Volume of two equal solid cones dropped into the vessel.

Volume of two equal solid cones dropped into the vessel = 492.8 cm³

Volume of one solid cone = $\dfrac{492.8}{2} = 246.4$ cm³.

Hence, the volume of each of the solid cone submerged is 246.4 cm³.