A uniform meter scale of mass 60 g, carries masses of 20 g, 30 g and 80 g from points 10 cm, 20 cm and 90 cm marks. Where must be the scale hanged with string to balance the scale?

Let, D be the point from where the scale is hanged so that the meter scale and the various masses are balanced.

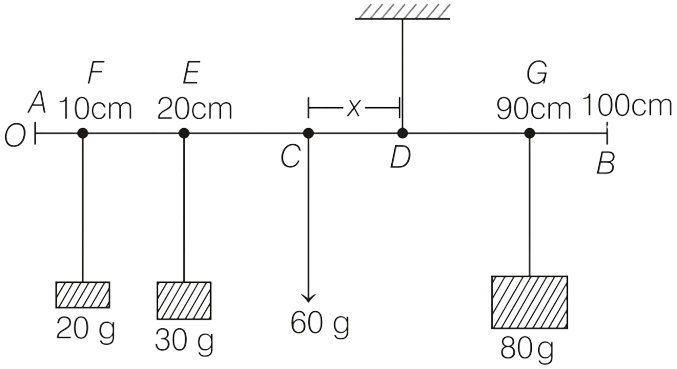
Clockwise moments = 80 x GD

Anticlockwise moments = (20 x FD) + (30 x ED) + (60 x CD)

As the meter scale is balanced.

∴ Sum of clockwise moments = sum of anticlockwise moments

80 x GD = (20 x FD) + (30 x ED) + (60 x CD)

[80 x {90 - (50 + x)}] = [20 x (50 + x - 10)] + [30 x (50 + x - 20)] + 60x

[80 x (90 - 50 - x)] = [20 x (50 + x - 10)] + [30 x (50 + x - 20)] + 60x

[80(40 - x)] = [20(40 + x)] + [30(30 + x)] + 60x

3200 - 80x = 800 + 20x + 900 + 30x + 60x

3200 - 80x = 800 + 20x + 900 + 30x + 60x

3200 - 80x = 1700 + 110x

3200 - 1700 = 110x + 80x

1500 = 190x

x = $\dfrac{1500}{190}$ = 7.89 ≈ 7.9 cm

Hence, the string should be hanged at 50 + 7.9 = 57.9 cm mark.