A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.

From figure,

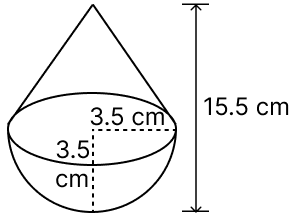
Height of cone (h) = 15.5 - 3.5 = 12 cm.

Radius of cone = Radius of hemisphere = r = 3.5 cm.

By formula,

Slant height (l) = $\sqrt{r^2 + h^2}$

Substituting values we get :

$l = \sqrt{(3.5)^2 + 12^2} \\[1em] = \sqrt{12.25 + 144} \\[1em] = \sqrt{156.25} \\[1em] = 12.5 \text{ cm}.$

Total surface area of toy = Curved surface area of cone + Curved surface area of hemisphere

= πrl + 2πr²

= πr(l + 2r)

= 3.5π(12.5 + 2 × 3.5)

= 3.5π(12.5 + 7)

= $3.5 \times \dfrac{22}{7} \times 19.5$

= 214.5 cm².

Hence, total surface area of toy = 214.5 cm².