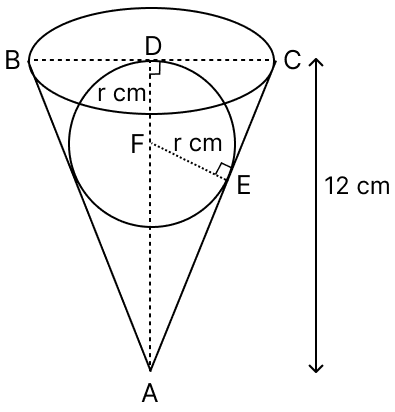
A sphere is placed in an inverted hollow conical vessel of base radius 5 cm and vertical height 12 cm. If the highest point of the sphere is at the level of the base of the cone, find the radius of the sphere. Show that the volume of the sphere and the conical vessel are as 40 : 81.

Given,

Radius of cone (R) = 5 cm.

Height of cone (H) = 12 cm

Let radius of sphere be r cm.

From figure,

FE = FD = r cm

AD = 12 cm, DC = 5 cm

Slant height (AC) = $\sqrt{AD^2 + CD^2} = \sqrt{12^2 + 5^2}$

= $\sqrt{144 + 25} = \sqrt{169}$ = 13 cm.

In △ADC and △AFE,

⇒ ∠ADC = ∠AEF (Both equal to 90°)

⇒ ∠A = ∠A (Common)

∴ △ADC ~ △AFE (By A.A. axiom)

Ratio of corresponding sides of similar triangle are equal.

$\therefore \dfrac{FE}{DC} = \dfrac{AF}{AC} \\[1em] \Rightarrow \dfrac{r}{5} = \dfrac{12 - r}{13} \\[1em] \Rightarrow 13r = 5(12 - r) \\[1em] \Rightarrow 13r = 60 - 5r \\[1em] \Rightarrow 18r = 60 \\[1em] \Rightarrow r = \dfrac{60}{18} = \dfrac{10}{3} \text{ cm}.$

Ratio of volume of sphere to volume of cone.

$\Rightarrow \dfrac{\text{Volume of sphere}}{\text{Volume of cone}} = \dfrac{\dfrac{4}{3}πr^3}{\dfrac{1}{3}πR^2H} \\[1em] = \dfrac{4r^3}{R^2H} \\[1em] = \dfrac{4 \times \Big(\dfrac{10}{3}\Big)^3}{5^2 \times 12} \\[1em] = \dfrac{4 \times \dfrac{1000}{27}}{25 \times 12} \\[1em] = \dfrac{4000}{25 \times 27 \times 12} \\[1em] = \dfrac{40}{81} = 40 : 81.$

Hence, proved that ratio of volume of sphere and conical vessel = 40 : 81.