A point P(a, b) is reflected in the x-axis to P'(2, -3), write down the values of a and b. P'' is the image of P, when reflected in the y-axis. Write down the coordinates of P''. Find the coordinates of P''', when P is reflected in the line, parallel to y-axis such that x = 4.

Since, P'(2, -3) is the image of P under reflection in the x-axis, from graph we get P(2, 3).

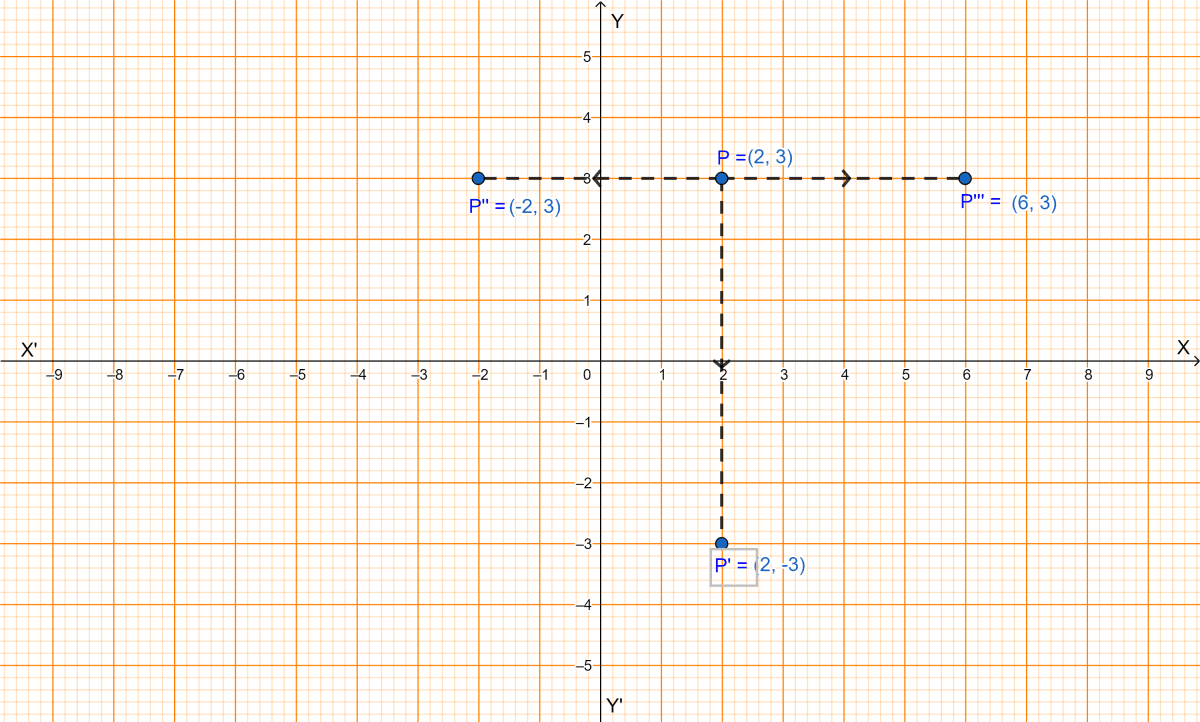
∴ The coordinates of P are (2,3), comparing with P(a, b) we get, a = 2 and b = 3.

We know that,

Rule to find reflection of a point in y-axis :

1. Change the sign of abscissa i.e. x-coordinate.
2. Retain the ordinate i.e. y-coordinate.

Since, P'' is image on reflection of P in y-axis.

∴ The coordinates of P'' are (-2,3).

We know that the reflection of the point (x, y) in the line x = a is the point (-x + 2a, y).

∴ The image of the point P(2, 3) under reflection in the line x = 4 is the point P'''(-2 + 2 × 4, 3) i.e the point P'''(6, 3).

Hence, the value of a = 2, b = 3 and the coordinates of P''(-2, 3), P'''(6, 3).