A field is 30 m long and 18 m broad. A pit 6 m long, 4 m wide and 3 m deep is dug out from the middle of the field and the earth removed is evenly spread over the remaining area of the field. Find the rise in the level of the remaining part of the field in centimeters correct to two decimal places.

From figure,

ABCD is a field.

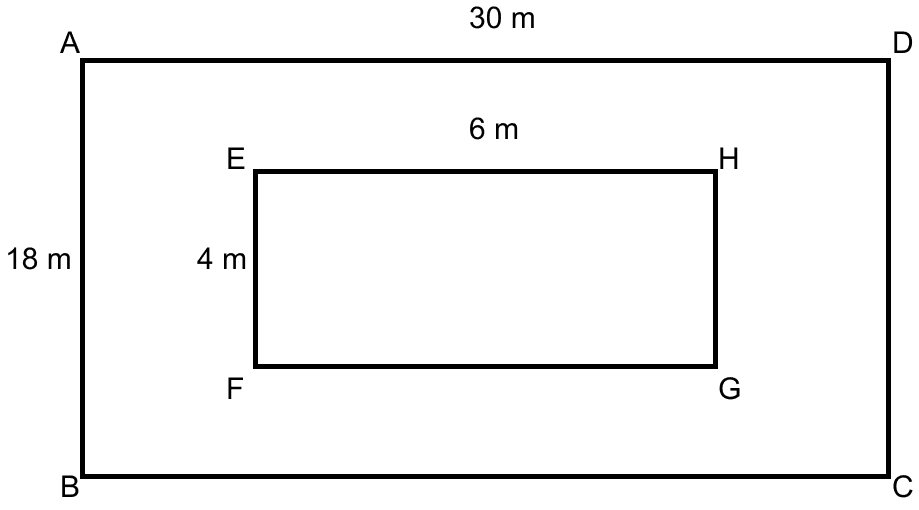
Volume of the earth dug out = 6 × 4 × 3 = 72 m³

Area of field ABCD = AB × BC = 18 × 30 = 540 m².

Area of pit EFGH = EF × FG = 4 × 6 = 24 m².

Area of remaining field = 540 - 24 = 516 m².

Let h metres is the level raised over the field uniformly.

Volume of rise in level = Volume of earth dug out

∴ Area of remaining field × h = 72

516h = 72

h = $\dfrac{72}{516} = 0.1395$ m = 13.95 cm

Hence, the level of the remaining field has been raised by 13.95 cm.