Mathematics
A cylindrical vessel with internal diameter 10 cm and height 10.5 cm is full of water. A solid cone of base diameter 7 cm and height 6 cm is completely immersed in water in the vessel. Find the volume of water left in the cylinder.
(Take )
Mensuration
1 Like
Answer
Given,
For cylindrical vessel :
Diameter = 10 cm
Radius (R) = = 5 cm.
Height (H) = 10.5 cm
For cone :
Diameter = 7 cm
Radius (r) = = 3.5 cm.
Height (h) = 6 cm
Volume of water left = Volume of cylinder - Volume of cone
= πR2H - πr2h
Hence, volume of water left in cylinder = 748 cm3.
Answered By
3 Likes
Related Questions
In an A.P., eight times of 8th term is equal to fifteen times the fifteenth term. Find the 23rd term of the A.P.
Using assumed mean method, calculate the mean.
Class-interval Frequency 0-30 22 30-60 30 60-90 40 90-120 36 120-150 28 150-180 20 Cards numbered 11 to 60 are kept in a box. If a card is drawn at random from the box, find the probability that the number on the drawn card is :
(i) a perfect square number
(ii) divisible by 5
(iii) a prime number less than 20.
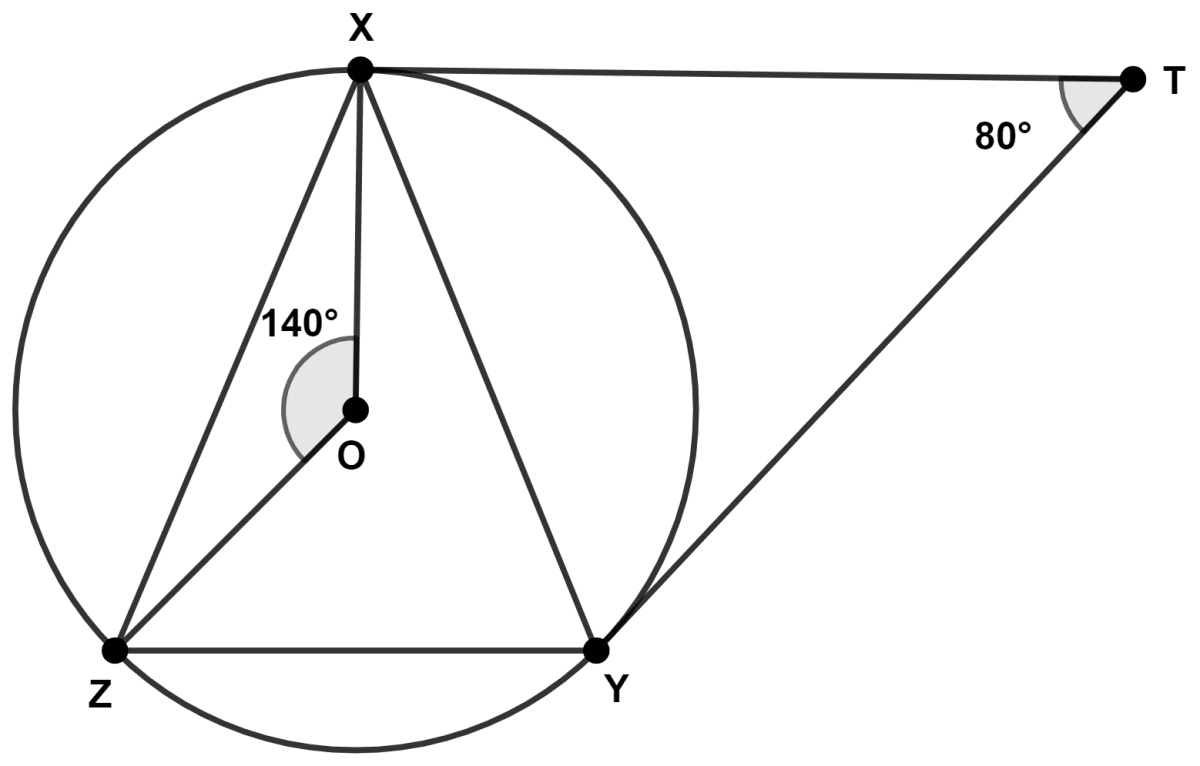
In the given figure, O is the center of the circumcircle of triangle XYZ. Tangents at points X and Y intersect at point T. If angle XTY = 80° and angle XOZ = 140°, find the angle ZXY.