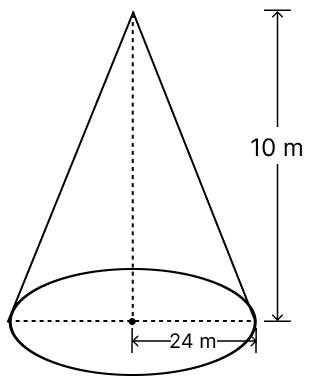
A conical tent is 10 m high and the radius of its base is 24 m. Find

(i) slant height of the tent.

(ii) cost of the canvas required to make the tent, if the cost of 1 m² canvas is ₹ 70.

(i) Given,

Radius of conical tent (r) = 24 m

Height of conical tent (h) = 10 m

By formula,

Slant height of conical tent (l) = $\sqrt{r^2 + h^2}$

Substituting values we get :

$l = \sqrt{(24)^2 + (10)^2} \\[1em] = \sqrt{576 + 100} \\[1em] = \sqrt{676} = 26 \text{ m}$

Hence, slant height of the conical tent is 26 m.

(ii) Given,

Curved surface area of the cone = πrl

= $\dfrac{22}{7}$ × 24 × 26

= $\dfrac{13728}{7}$ m²

The cost of the canvas required to make the tent, at ₹ 70 per m² = Curved surface area of the cone x ₹ 70

= $\dfrac{13728}{7}$ × 70

= ₹ 137280.

Hence, the cost of the canvas is ₹ 137280.