Physics
A coin is placed at the bottom of a beaker containing water (refractive index = 4/3) at a depth of 16 cm. By what height the coin appears to be raised when seen from vertically above?
Refraction Plane Surfaces
67 Likes
Answer
As we know,
aμm})
Given,
and
Real depth = 16 cm
So, substituting the values in the formula we get,
Hence, the coin appears to be raised by a height of 4 cm when seen from vertically above.
Answered By
30 Likes
Related Questions
A student puts his pencil into an empty trough and observes the pencil from the position as indicated in the figure.
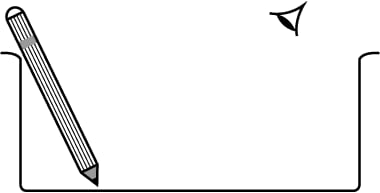
(i) What change will be observed in the appearance of the pencil when water is poured into the trough?
(ii) Name the phenomenon which accounts for the above-started observation.
(iii) Complete the diagram showing how the student’s eye sees the pencil through water.
A water pond appears to be 3 m deep. If the refractive index of water is 4/3, find the actual depth of the pond.
A postage stamp kept below a rectangular glass slab of refractive index 1.5 when viewed from vertically above it, appears to be raised by 7.0 mm. Calculate the thickness of the glass slab.
At angle of incidence equal to the critical angle, the angle of refraction is:
- 0°
- 30°
- 90°
- 180°