Mathematics
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Circles
2 Likes
Answer
In figure,
A, D and S denote the positions of Ankur, David and Syed, respectively sitting at equal distance.
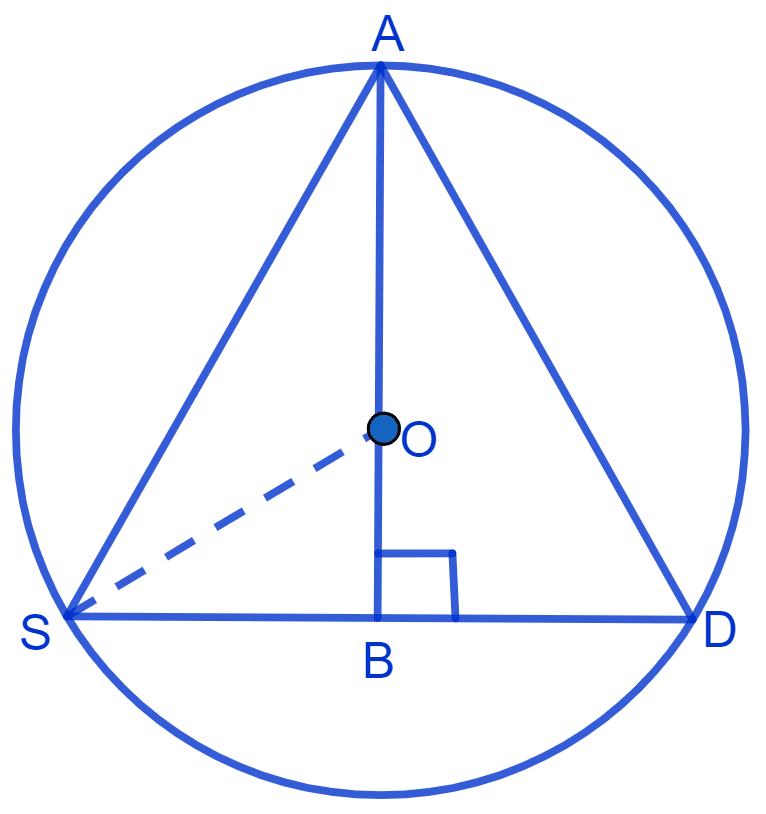
We know that,
If two minor arcs are equal in measure, then their corresponding chords are equal in measure.
∴ AD = DS = SA = 2x (let).
∴ ∆ ADS is an equilateral triangle.
From figure,
Radius = OA = OS = 20 m
Draw AB perpendicular to chord SD.
We know that,
Perpendicular from center bisects the chord.
∴ AB is the median.
∴ BS = BD = = x.
We know that,
Centre and Centroid are the same for an equilateral triangle, and it divides the median in the ratio 2 : 1.
∴ OA : OB = 2 : 1
= 10 m.
From figure,
AB = OA + OB = 20 + 10 = 30 m.
In right angle triangle ASB,
By pythagoras theorem,
⇒ AS2 = AB2 + BS2
⇒ (2x)2 = 302 + x2
⇒ 4x2 = 900 + x2
⇒ 4x2 - x2 = 900
⇒ 3x2 = 900
⇒ x2 =
⇒ x2 = 300
⇒ x =
⇒ 2x = .
Hence, the length of the string of each phone = m.
Answered By
1 Like
Related Questions
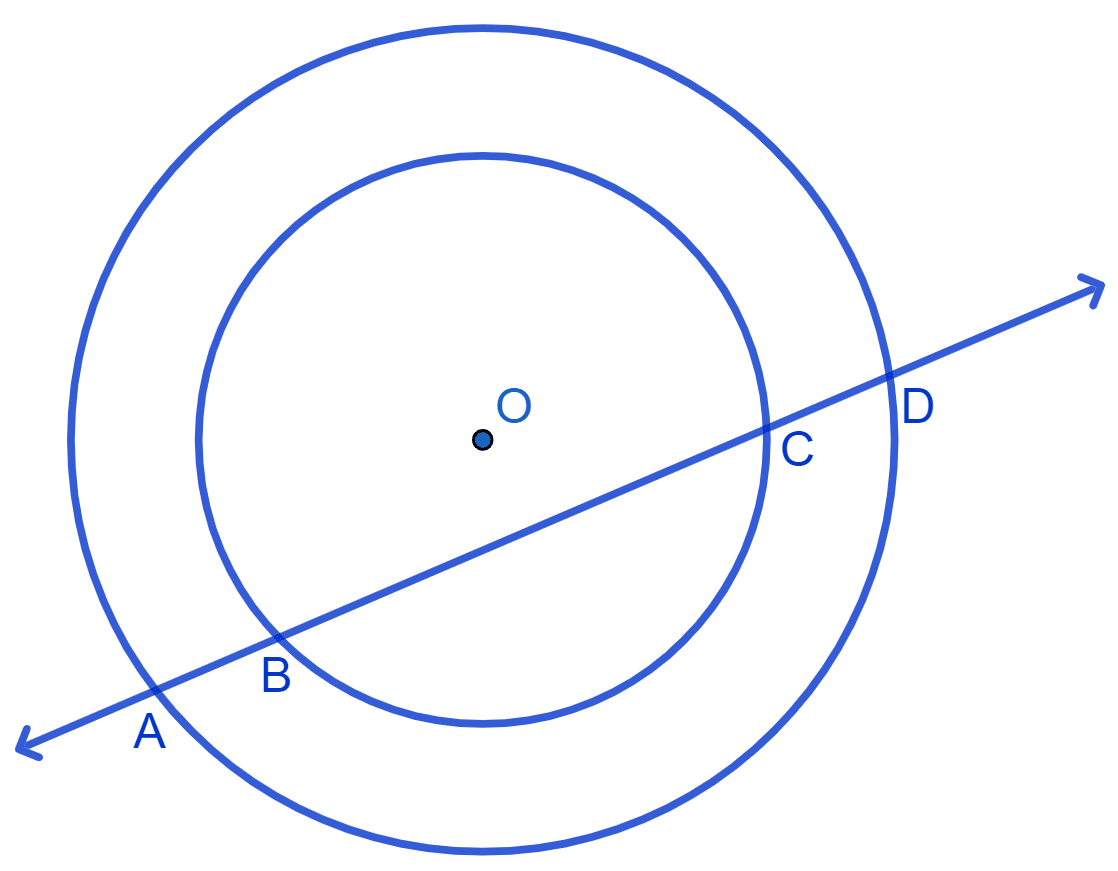
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD.
Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip?
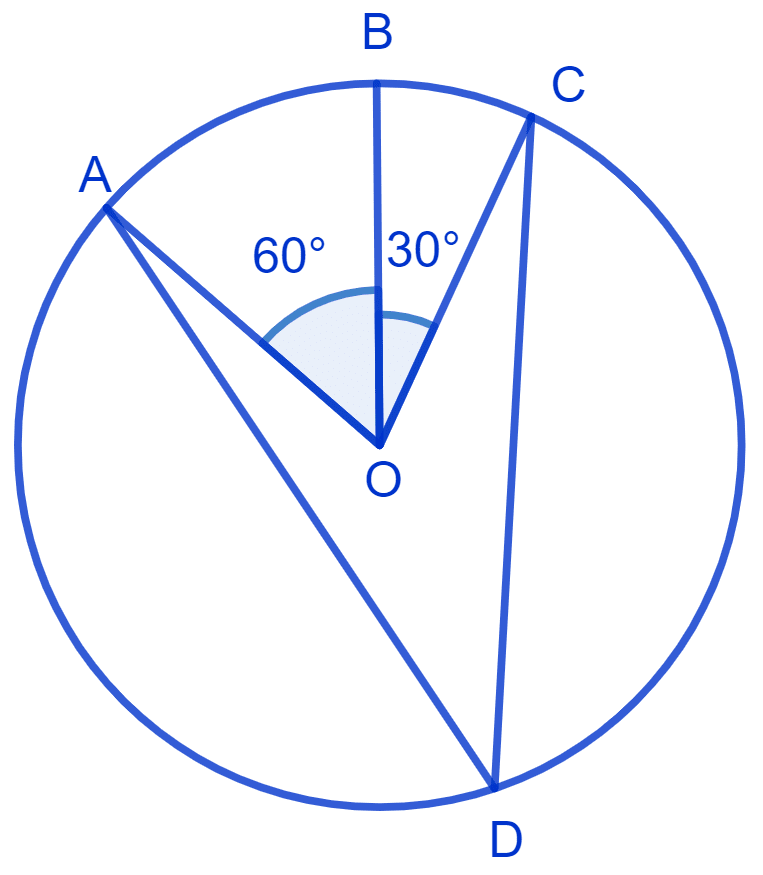
In Fig. A, B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.